Electronics and Communication Engineering - Exam Questions Papers

Exercise :: Exam Questions Papers - Exam Paper 12

26.

Figure shows four D type FFs are connected as a shift register using an XOR gate. The initial state and 3 subsequent states for 3 clock pulses are also given

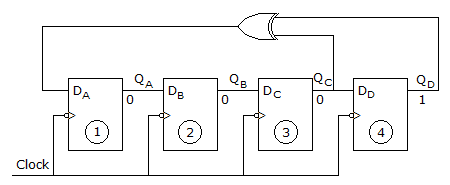
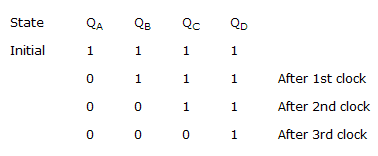
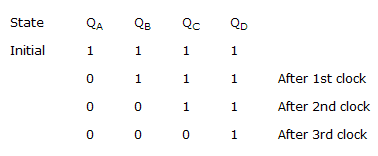
The state Q_A Q_B Q_C Q_D after the 4th clock pulse is

A.	0000
B.	1111
C.	1001
D.	1000

Answer: Option D

Explanation:

After the 3rd pulse FF3 is 0 and FF4 is 1, so that XOR output is 1 which is fed to DA.

So, Q_A = 1, Q_A to Q_B → 0

A_B to A_C → 0, Q_C → Q_D → 0.

27.

A rectangular wave guide is designed to propagate at the dominant mode TE₁₀ at a frequency of 5 GHz. The cut-off frequency is 0.8 of signal frequency. The ratio of the guide width to height is 2. The dimensions of the guide are

A.	3.75 cm, 1.875 cm
B.	4 cm, 2 cm
C.	8 cm, 4 cm
D.	2.54 cm, 1.27 cm

Answer: Option A

Explanation:

λ_c = 2a or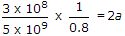

⇒ a = 3.75 cm

Also,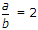

∴ .

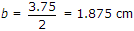28.

In the Taylor series expansion of exp(x) + sin(x) about the point x = p, the coefficient of (x - p)² is

A.	exp (p)
B.	0.5 exp (p)
C.	exp (p) + 1
D.	exp (p) - 1

Answer: Option B

Explanation:

f(x) = e^x + sin x

Coefficient of (x - p)² = 1 / 2! f''(x)

f'(x) = e^x + cos x

f'(x) = e^x - sin x

f''(x)|_x=p = e^p

Thus coefficient of (x - p)² = 0.5 .

29.

The Z transform of a particular signal is given as

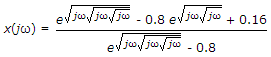
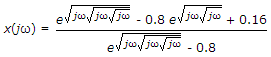
The practical implementation of the system will be

A.	non causal and stable
B.	causal and stable
C.	unstable and noncausal
D.	can't say

Answer: Option B

Explanation:

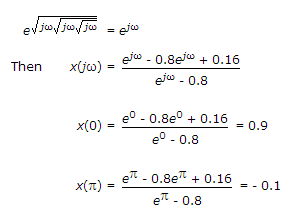
When get high value at ω = 0, and low value at ω = p, hence we get a low pass filter.

So the system is min-phase causal system. For practical implementation of the system, the system has to be stable.

30.

If g(t) = e^-pt² then G(1/p) is __________ where g(t) G(f)

A.	e^-2/p
B.	e^-1/p
C.	e^-p
D.	e^2p

Answer: Option B

Explanation:

The signal g(t) given above is a gaussian pulse and it satisfies the relation

g(t) = - 2pt g(t)

∴ Its fourier transform is same as the signal itself in frequency domain

G(f) = e^-pf²

G(1/p) = e^-p(1/p)² = e^-1/p.

Current Affairs 2022

Interview Questions and Answers