IndiaBIX

Electronics and Communication Engineering - Exam Questions Papers

Exercise : Exam Questions Papers - Exam Paper 9
1.
If X = 1 in the logic equation [X + Z { Y + (Z + X Y)}] { X + Z (X + Y)} = 1, then
Y = Z
Y = Z
Z = 1
Z = 0
Answer: Option
Explanation:

[1 + z{y + z + y}][0 + z] = 1, z = 1, z = 0.

2.
(22)4 + (101)3 - (20)5 = (x)4 + (4)x+1 where x > 4. The value of x is
6
4
12
8
Answer: Option
Explanation:

(22)4 + (10)10 - (10)10 = (22)4

Since x > 4, i.e. all the number systems with base greater than 4.

All these will contain symbol '4' which will have same value in all bases.

Converting 4 into base '4'

system (4)10 (10)4

Now (22)4 = (x)4 + (10)4

∴ (x)4 = (22)4 - (10)4 = (12)4

∴ x = 12.

3.
Consider a system with the transfer function . Its damping ratio will be 0.5 when the value of k is :
2/6
3
1/6
6
Answer: Option
Explanation:

ξ = 0.5,

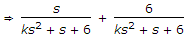
We take second term only

.

4.
For the system with given characteristic equation
s5 + 4s4 + 8s3 + 8s2 + 7s + 4 = 0
The number of roots on left hand side, right hand side and imaginary axis are respectively.
3, 2, 0
4, 0, 1
3, 0, 2
4, 1, 0
Answer: Option
Explanation:

Apply Routh Hurwitz criteria.

5.
A series RLC circuit has a resonance frequency of 1 kHz and a quality factor Q = 100. If each of R, L and C is doubled from its original value, the new Q of the circuit is
25
50
100
200
Answer: Option
Explanation:

Resonant frequency

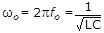
Quality factor =

where R, L, C all are doubled, then

.

Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers