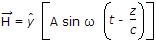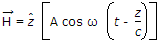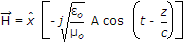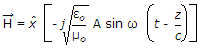Electronics and Communication Engineering - Exam Questions Papers
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 22
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 2
Potential due to surface charge
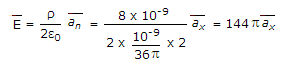
∴ 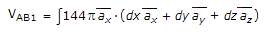
∴ 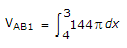
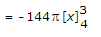 = 144pv = 452.16v
= 144pv = 452.16v
Potential due to line charge at x = 1 and y = 2
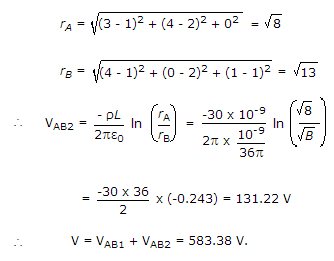
Truth table of X-NOR gate :
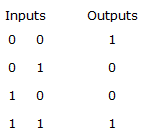
i.e. when an input to the X-NOR gate is '0' then the other input to the gate is complemented at the output.
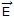 of a wave in free space (εo, μo) is
of a wave in free space (εo, μo) is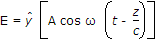
Its magnetic field vector
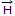 will be given by
will be given by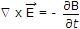
Now 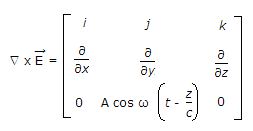
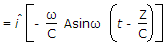
∴ 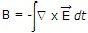
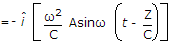 (use B = μ0 H) .
(use B = μ0 H) .
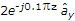 A/m. If the velocity of the wave is 2 x 108 m/s and εr = 1.8, then. The frequency of the wave is
A/m. If the velocity of the wave is 2 x 108 m/s and εr = 1.8, then. The frequency of the wave is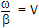
r = 0.1p
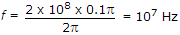 .
.
The autocorrelation function of z(t) is given by
Rz(t, u) = E[Z(t)Z(u)]
= E[(x(t) + y(t)) (x(u) + y(u))]
= E[x(t) x (u)] + E[x(t) y(u)] + E[y(t) x(u)] + E[y(t) y(u)]
= Rx(E, u) + Rxy(t, u) + Ryx(t, u) + Ry(t, u)
Defining t = t - u, we may therefore write Rz(t) = Rx(t) + Rxy(t) + Ryx(t) + Ry(t).
When the random process x(t) and y(t) are also jointly stationary.
Accordingly, taking the fourier transform of both sides of equation we get
Sz(f = Sx(f) + Sxy(f) + Syx(f) + Sy(f)
We thus see that the cross spectral densities Sxy(f) and Syx(f) represent the spectral components that must be added to the individual power spectral densities of a pair of correlated random processes in order to obtain the power spectral density of their sum.
When the stationary process x(t) and y(t) are uncorrelated the cross-sectional densities Sxy(f) and Syz(f) are zero
∴ Sz(f) = Sx(f) + Sy(f).