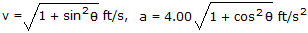Online Engineering Mechanics Test - Engineering Mechanics Test 2
- This is a FREE online test. Beware of scammers who ask for money to attend this test.
- Total number of questions: 20.
- Time allotted: 30 minutes.
- Each question carries 1 mark; there are no negative marks.
- DO NOT refresh the page.
- All the best!
Marks : 2/20
Test Review : View answers and explanation for this test.
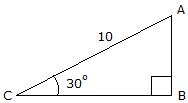
Using the basic trigonomic functions, determine the length of side AB of the right triangle.
Express the Force F2 in Cartesian vector form.
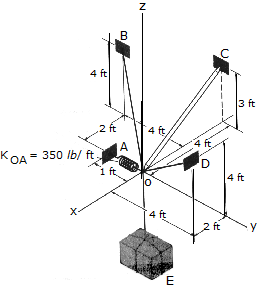
Determine the tension developed in cables OD and OB and the strut OC, required to support the 500-lb crate. The spring OA has an unstretched length of 0.2 ft and a stiffness of kOA = 350lb/ft. The force in the strut acts along the axis of the strut.
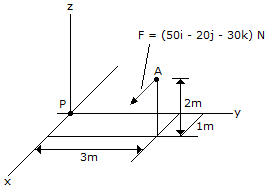
Replace the force at A by an equivalent force and couple moment at P. Express the results on Cartesian vector form.
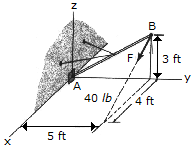
Replace the force F, having a magnitude of F = 40 lb and acting at B, by an equivalent force and couple moment at A.
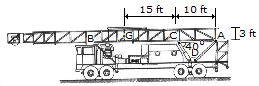
The oil rig is supported on the trailer by the pin or axle at A and the frame at B. If the rig has a weight of 115,000 lb and the center of gravity at G, determine the force F that must de developed along the hydraulic cylinder CD in order to start lifting the rig (slowly) off B toward the vertical. Also compute the horizontal and vertical components of reaction at the pin A.
Determine the internal axial force, shear force, and moment at point F of the frame.
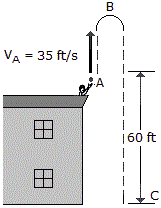
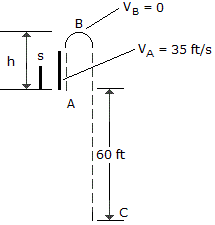
A ball thrown vertically upward from the top of a building with an initial velocity of vA = 35 ft/s. Determine (a) how high above the top of the building the ball will go before it stops at B, (b) the time tAB it takes to reach its maximum height, and (c) the total time tAC needed for it to reach the ground at C from the instant it is released.
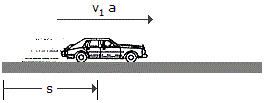
A car, initially at rest, moves along a straight road with constant acceleration such that it attains a velocity of 60 ft/s when s = 150 ft. Then after being subjected to another constant acceleration, it attains a final velocity of 100 ft/s when s = 325 ft. Determine the average velocity and average acceleration of the car for the entire 325-ft displacement.
The cylindrical cam C is held fixed while the rod AB and bearings E and F rotate about the vertical axis of the cam at a constant rate of 
= 4 rad/s. If the rod is free to slide through the bearings, determine the magnitudes of the velocity and acceleration of the guide D on the rod as a function of . The guide follows the groove in the cam, and the groove is defined by the equations r = 0.25 ft and z = (0.25 cos ) ft.
ft/s, a = 4.00 sin ft/s2 ft/s, a = 4.00 cos ft/s2
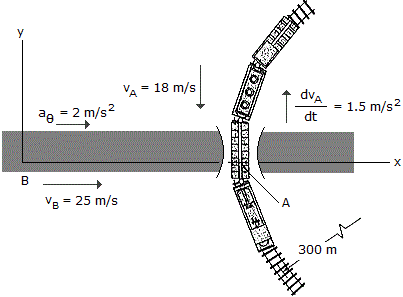
A passenger in the automobile B observes the motion of the train car
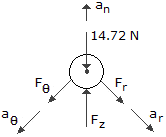
A particle having a mass of 1.5 kg, moves along a three-dimensional path defined by the equations r = 94 + 3t) m, = (t2 + 2) rad, and z = (6 - t3) m, where t is in seconds, and the z-axis is vertical. Determine the r, , and z components of force which the path exerts on the particle when t = 2 s.
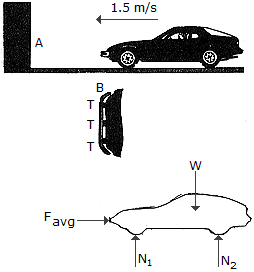
A car is equipped with a bumper B designed to absorb collisions. The bumper is mounted to the car using pieces of flexible tubing T. Upon collision with a rigid barrier A, a constant horizontal force F is developed which causes a car deceleration of 3g = 29.43 m/s2 (the highest safe deceleration for a passenger without a seatbelt). If the car and passenger have a total mass of 1.5 Mg and the car is initially coasting with a speed of 1.5 m/s, compute the magnitude of F needed to stop the car and the deformation x of the bumper tubing.
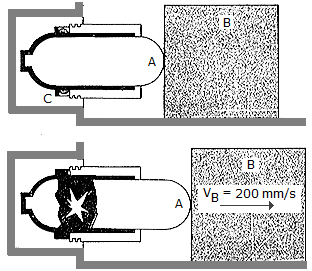
In cases of emergency, the gas actuator can be used to move a 75-kg block B by exploding a charge C near a pressurized cylinder of negligible mass. As a result of the explosion, the cylinder fractures and the released gas forces the front part ofthe cylinder, A, to move B and the floor is 
= 0.5, determine the impulse that the actuator must impart to B.
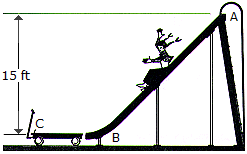
A girl having a weight of 40 lb slides down the smooth slide onto the surface of a 20-lb wagon. Determine the speed of the wagon at the instant the girl stops sliding on it. If someone ties the wagon to the slide at B, determine the horizontal impulse the girl will exert at C in order to stop her motion. Neglect friction and assume that the girl starts from rest at the top of the slide, A.
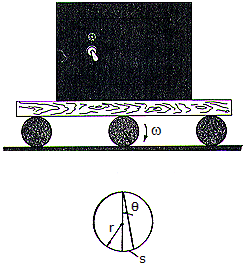
The safe is transported on a platform which rests on rollers, each having a radius r. If the rollers do not slip, determine their angular velocity 
if the safe moves forward with a velocity v.
= v/(2r) = v/r = 3v/r = 2v/r
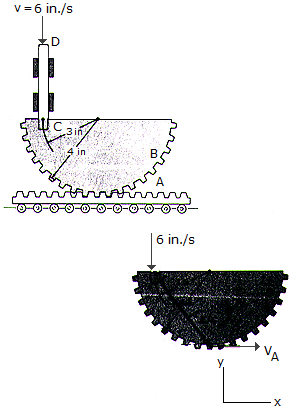
If rod CD has a downward velocity of 6in/s at the instant shown, determine the velocity of the gear rack A at this instant. The rod is pinned at C to gear B.
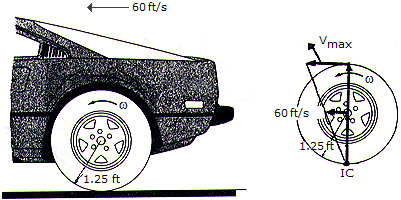
The automobile with wheels 2.5 ft in diameter is traveling in a straight path at a rate of 60 ft/s. If no slipping occurs, determine the angular velocity of one of the rear wheels and the velocity of the fastest moving point on the wheel.
= 48 rad/s, vmax = 84.9 ft/s = 24 rad/s, vmax = 84.9 ft/s = 48 rad/s, vmax = 120.0 ft/s = 24 rad/s, vmax = 120.0 ft/s
A cord wrapped around the inner core of a spool. If the cord is pulled with a constant tension of 30 lb and the spool is originally at rest, determine the spool's angular Velocity when s = 8 ft of cord have unraveled. Neglect the weight of the cord. The spool and cord have a total weight of 400 lb and the radius of gyration about the axle A is kA = 1.30 ft.
= 6.73 rad/s = 3.38 rad/s = 4.78 rad/s = 11.43 rad/s