Seats for Mathematics, Physics and Biology in a school are in the ratio 5 : 7 : 8. There is a proposal to increase these seats by 40%, 50% and 75% respectively. What will be the ratio of increased seats?
A.
2 : 3 : 4
B.
6 : 7 : 8
C.
6 : 8 : 9
D.
None of these
Answer: Option A
Explanation:
Originally, let the number of seats for Mathematics, Physics and Biology be 5x, 7x and 8x respectively.
Number of increased seats are (140% of 5x), (150% of 7x) and (175% of 8x).
Each of these questions is followed by three statements. You have to study the question and all the three statements given to decide whether any information provided in the statement(s) is redundant and can be dispensed with while answering the given question.
5.
Three friends, P, Q and R started a partnership business investing money in the ratio of 5 : 4 : 2 respectively for a period of 3 years. What is the amount received by P as his share profit?
I.
Total amount invested in the business in Rs. 22,000.
II.
Profit earned at the end of 3 years is of the total investment.
III.
The average amount of profit earned per year is Rs. 2750.
A.
I or II or III
B.
Either III only, or I and II together
C.
Any two of the three
D.
All I, II and III are required.
E.
None of these
Answer: Option B
Explanation:
I and II give, profit after 3 years = Rs.
3
x 22000
= Rs. 8250.
8
From III also, profit after 3 years = Rs. (2750 x 3) = Rs. 8250.
P's share = Rs.
8250 x
5
= Rs. 3750.
11
Thus, (either III is redundant [or] I and II are redundant).
P can complete a work in 12 days working 8 hours a day. Q can complete the same work in 8 days working 10 hours a day. If both P and Q work together, working 8 hours a day, in how many days can they complete the work?
A.
5
5
11
B.
5
6
11
C.
6
5
11
D.
6
6
11
Answer: Option A
Explanation:
P can complete the work in (12 x 8) hrs. = 96 hrs.
Q can complete the work in (8 x 10) hrs. = 80 hrs.
Two trains, each 100 m long, moving in opposite directions, cross each other in 8 seconds. If one is moving twice as fast the other, then the speed of the faster train is:
A train travelling at a speed of 75 mph enters a tunnel 3 miles long. The train is mile long. How long does it take for the train to pass through the tunnel from the moment the front enters to the moment the rear emerges?
A man takes twice as long to row a distance against the stream as to row the same distance in favour of the stream. The ratio of the speed of the boat (in still water) and the stream is:
Each of these questions is followed by three statements. You have to study the question and all the three statements given to decide whether any information provided in the statement(s) is redundant and can be dispensed with while answering the given question.
15.
What is the cost painting the two adjacent walls of a hall at Rs. 5 per m2 which has no windows or doors?
I.
The area of the hall is 24 sq. m.
II.
The breadth, length and height of the hall are in the ratio of 4 : 6 : 5 respectively.
III.
Area of one wall is 30 sq. m.
A.
I only
B.
II only
C.
III only
D.
Either I or III
E.
All I, II and III are required.
Answer: Option C
Explanation:
From II, let l = 4x, b = 6x and h = 5x.
Then, area of the hall = (24x2) m2.
From I. Area of the hall = 24 m2.
From II and I, we get 24x2 = 24 x = 1.
l = 4 m, b = 6 and h = 5 m.
Thus, area of two adjacent walls = [(l x h) + (b x h)] m2 can be found out and so the cost of painting two adjacent walls may be found out.
Each of the questions given below consists of a statement and / or a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statement(s) is / are sufficient to answer the given question. Read the both statements and
Give answer (A) if the data in Statement I alone are sufficient to answer the question, while the data in Statement II alone are not sufficient to answer the question.
Give answer (B) if the data in Statement II alone are sufficient to answer the question, while the data in Statement I alone are not sufficient to answer the question.
Give answer (C) if the data either in Statement I or in Statement II alone are sufficient to answer the question.
Give answer (D) if the data even in both Statements I and II together are not sufficient to answer the question.
Give answer(E) if the data in both Statements I and II together are necessary to answer the question.
16.
What is the height of a circular cone?
I.
The area of that cone is equal to the area of a rectangle whose length is 33 cm.
II.
The area of the base of that cone is 154 sq. cm.
A.
I alone sufficient while II alone not sufficient to answer
B.
II alone sufficient while I alone not sufficient to answer
C.
Either I or II alone sufficient to answer
D.
Both I and II are not sufficient to answer
E.
Both I and II are necessary to answer
Answer: Option D
Explanation:
II gives the value of r.
But, in I, the breadth of rectangle is not given.
So, we cannot find the surface area of the cone.
Hence, the height of the cone cannot be determined.
Loading Test...
Required number = (90 x 4) + 4 = 364.
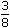of the total investment.
250 x x = (200 x 60)
miles long. The train is 
mile long. How long does it take for the train to pass through the tunnel from the moment the front enters to the moment the rear emerges?
% stock at 117?