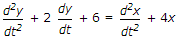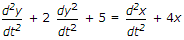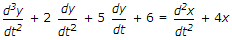Electronics and Communication Engineering - Exam Questions Papers
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 22
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 2
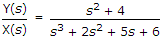 The differential equation representing the system is
The differential equation representing the system is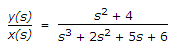
(s3 + 2s2 + 5s + 6)y(s) = (s2 + 4) x (s)
s3y(s) + 2s2y(s) + 5sy(s) + 6y(s) = s2 x (s) + 4 x (s)
Replacing s by 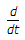 and y(s) by y(t) and x(s) by x(t) we get
and y(s) by y(t) and x(s) by x(t) we get
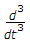 y(t) + 2
y(t) + 2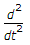 y(t) + 5
y(t) + 5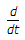 y(t) + 6y(t)
y(t) + 6y(t)
= 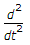 x(t) + 4x(t)
x(t) + 4x(t)
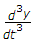 + 2
+ 2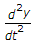 + 5
+ 5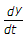 + 6 =
+ 6 = 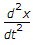 + 4x
+ 4x
This is required differential equation.
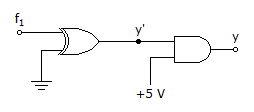
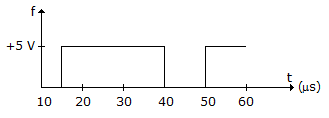
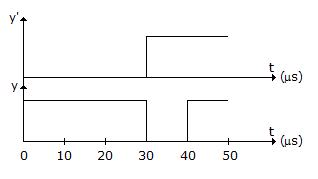
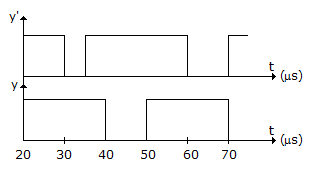
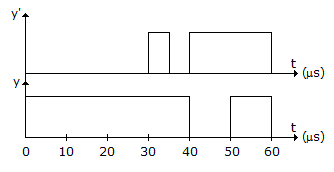
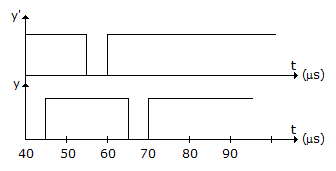
Logic gates are 20 μs and 10 μs respectively, then the wave y' and y (with initial condition y = 1) will be :
Since y is at logic '1' initially, y' must be at logic '1'.
Also, one input of the EXOR gate is tied to zero therefore 'f' will be directly transferred to the output.
The logic gates will introduce gate delays which will lead to the answer .
Ic = 8 A
m = 0.8
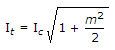
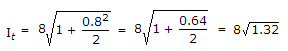
= 8 x 1.149 = 9.19 A.
Maximum data rate for noiseless channel is given by Nyquist Theorem
= 2H log2 V bits/sec
V - discrete levels (Here Binary i.e. 2)
H - Bandwidth
∴ Maximum data rate = 2H log2 V
= 2(3 KHz) log2 2 = 2 x 3 x 103 x 1
= 6 x 103 = 6000 bps.
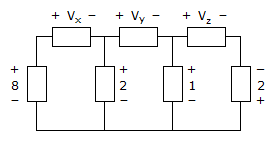
Apply Mesh analysis
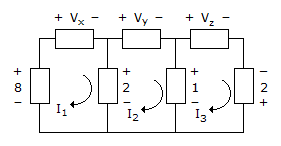
Apply KVL to mesh 2
-2 + Vy + 1 = 0
∴ Vy = 1
Apply KVL to mesh 1
∴ -8 + Vx + 2 = 0
∴ Vx = 6 V
Apply KVL to mesh 3
-1 + Vz -2 = 0
∴ Vz = 3 V.