Online Engineering Mechanics Test - Engineering Mechanics Test 4
- This is a FREE online test. Beware of scammers who ask for money to attend this test.
- Total number of questions: 20.
- Time allotted: 30 minutes.
- Each question carries 1 mark; there are no negative marks.
- DO NOT refresh the page.
- All the best!
Marks : 2/20
Test Review : View answers and explanation for this test.

Determine the magnitudes of the resultant force and its direction measured from the positive x axis.

Express each force in Cartesian vector form.

The ball joint is subjected to the three forces shown. Find the magnitude of the resultant force.

Determine the projection of the position vector r along the aa axis.

Determine the magnitude and direction of the moment of the force at A about point P.
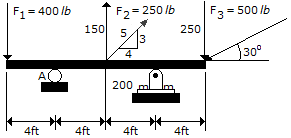
Determine the moment of force F3 about point A on the beam.
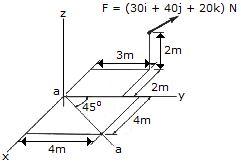
Determine the magnitude of the projection of the moment cause by the force about the aa axis.

Determine the magnitude and direction of the couple shown.
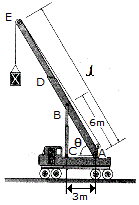
The crane provides a long-reach capacity by using the telescopic boom segment DE. The entire boom is supported by a pin at A and by the telescopic hydraulic cylinder BC, which can be considered as a two-force member. The rated load capacity of the crane is measured by a maximum force developed in the hydraulic cylinder. If this maximum force is developed when the boom supports a mass m = 6 Mg and its length is l = 40 and  = 60°, determine the greatest mass that can be supported when the boom length is extended to l = 50 m and
= 60°, determine the greatest mass that can be supported when the boom length is extended to l = 50 m and  = 45°. Neglect the weight of the boom and the size of the pulley at E. Assume the crane does not overturn. Note: when
= 45°. Neglect the weight of the boom and the size of the pulley at E. Assume the crane does not overturn. Note: when  = 60° BC is vertical; however, when
= 60° BC is vertical; however, when  = 45° this is not the case.
= 45° this is not the case.

A crane is constructed from two side trusses. If a load of 4 kN is suspended from one of these trusses as shown, determine the force in members FG, GK, and <KJ. State whether the members are in tension or compression. Assume the joints are pin-connected.

The block B is suspended from a cable that is attached to the block at E, wraps around three pulleys, and is tied to the back of a truck. If the truck starts from rest when xD is zero, and moves forward with a constant acceleration of aD = 2 m/s2, determine the speed of the block at the instant xD = 3 m.
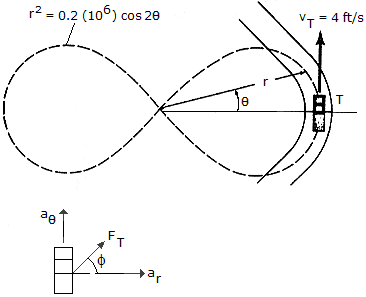
A truck T has a weight of 8,000 lb and is traveling along a portion of a road defined by the lemniscate r2 = 0.2(106) cos 2  , where r is measured in feet and
, where r is measured in feet and  is in radians. If the truck maintains a constant speed of vr = 4 ft/s, determine the magnitude of the resultant frictional force which must be exerted by all the wheels to maintain the motion when
is in radians. If the truck maintains a constant speed of vr = 4 ft/s, determine the magnitude of the resultant frictional force which must be exerted by all the wheels to maintain the motion when  = 0.
= 0.
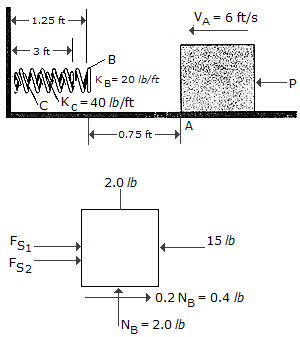
The coefficient of friction between the 2-lb block and the surface is  = 0.2. The block is acted upon by a horizontal force of P. Determine the maximum deformation of the outer spring B at the instant the block comes to rest. Spring B has a stiffness of KB = 20 lb/ft and the "nested" spring C has a stiffness of kc = 40 lb/ft.
= 0.2. The block is acted upon by a horizontal force of P. Determine the maximum deformation of the outer spring B at the instant the block comes to rest. Spring B has a stiffness of KB = 20 lb/ft and the "nested" spring C has a stiffness of kc = 40 lb/ft.
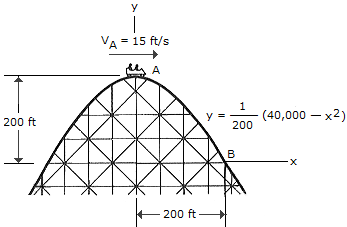
The roller-coaster car has a speed of 15 ft/s when it is at the crest of a vertical parabolic track. Compute the velocity and the normal force it exerts on the track when it reaches point B. Neglect friction and the mass of the wheels. The total weight of the car and the passengers is 350 lb.
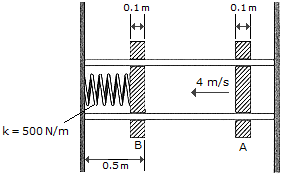
Plates A and B each have a mass of 4 kg and are restricted to move along the frictionless guides. If the coefficient of restitution between the plates is e = 0.7, determine (a) the speed of both plates just after collision and (b) the maximum deflection of the spring. Plate A has a velocity of 4 m/s just before striking B. Plate B is originally at rest.
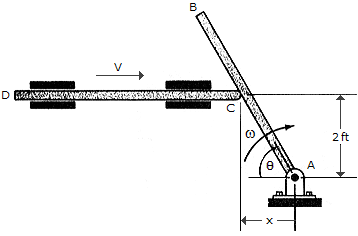
Rod CD presses against AB, giving it an angular velocity. If the angular velocity of AB is maintained at  = 5 rad/s, determine the required speed v of CD for any angle
= 5 rad/s, determine the required speed v of CD for any angle  of rod AB.
of rod AB.
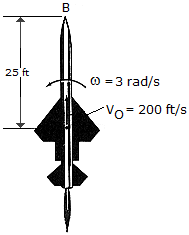
Due to an engine failure, the missile is rotating at  = 3 rad/s, while its mass center G is moving upward at 200 ft/s. Determine the magnitude of the velocity of its nose B at this instant.
= 3 rad/s, while its mass center G is moving upward at 200 ft/s. Determine the magnitude of the velocity of its nose B at this instant.

The sports car has a mass of 1.5 Mg and a center of mass at G. Determine the shortest time it takes for it to reach a speed of 80 km/h, starting from rest, if the engine only drives the rear wheels, whereas the front wheels are free rolling. The coefficient of friction between the wheels and road is  = 0.2. Neglect the mass of the wheels for the calculation.
= 0.2. Neglect the mass of the wheels for the calculation.
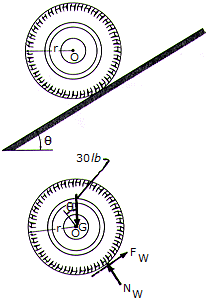
The wheel has a weight of 30 lb, a radius of r = 0.5 ft, and a radius of gyration of kG = 0.23 ft. If the coefficient if friction between the wheel and the plane is  = 0.2, determine the wheel's angular acceleration as it rolls down the incline. Set
= 0.2, determine the wheel's angular acceleration as it rolls down the incline. Set  = 12°.
= 12°.


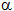 = 59.5 rad/s2
= 59.5 rad/s2