Electronics and Communication Engineering - Exam Questions Papers
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 22
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 2
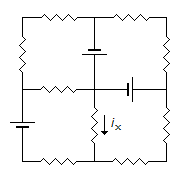
Using Mesh analysis
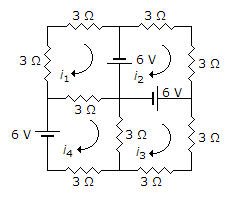
Loop 1 : 6 = 9i1 - 3i4 ...(i)
Loop 2: 6 + 6 = - 6i2
i2 = - 2A ...(ii)
Loop 3: 6 = 9i3 - 3i4 ...(iii)
Loop 4: 6 = 9i4 - 3i3 - 3i1 ...(iv)
Solving the above equations simultaneously
i1 = i3 = 1.1428 A
i4 = 1.432 A
∴ ix = i4 - i3 = 0.2892 A.
Picture elements (pixel) = 512 x 512 = 262144
Information per picture element N = log2 M
M = 2N
8 = 2N
N = 3
Information for 262144 pixels = 262144 x 3 = 786432 bits
Entropy is same as average information per message.
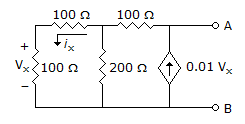
Since there is no independent source in the network
VTH = O V
To find RTh apply : A current source of 1 A across A and B.
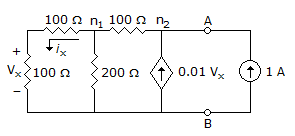
Apply KCL at node n1
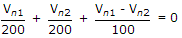
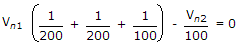
Apply KCL at node Vn2
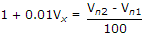
Vn1 = 2Vx put in (i)
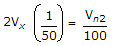
∴ Vn2 = 4vx
put in (ii)
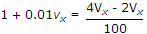
100 + Vx = 2Vx
100 = Vx
∴ Vn2 = 4Vx = 400 V
∴ 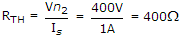 .
.
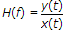 then for this to be true x(t) is __________ .
then for this to be true x(t) is __________ .Consider x(t) = ej2pft
y(t) = h(t) * x (t)
⇒ y(t) =  h(t). ej2pf(t - t) . dt
h(t). ej2pf(t - t) . dt
= ei2pft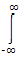 h(t) . e- j2pft . dt
h(t) . e- j2pft . dt
= ej2pft x H(f) = x(t) x H(f)
⇒ 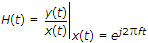 .
.

Dual of R → G




