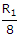Electronics and Communication Engineering - Exam Questions Papers
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 22
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 2
The range of the radar is directly proportional to the square root of the frequency.
∴ R ∝ 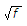
∴ R1 ∝ 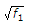
and R2 ∝ 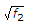
∴ 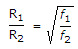
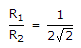
∴ 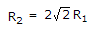 .
.
 ; which of the following figure shows an exact field distribution?
; which of the following figure shows an exact field distribution?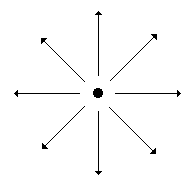
The given figure fails to show the symmetry with respect to Φ.

The figure shows symmetry with respect to f, also the length of arrow is decreasing away from the charge shows that magnitude E is decreasing away from line charge.
But problem with this figure is longest lines must be shown in most crowded region.

Here we use lines of fixed segments but different thickness. But this attempt also makes the region crowded near origin.

This figure shows compromise. A symmetrical distribution of lines (at every 45°) shows azimuthal symmetry and arrowheads show direction.
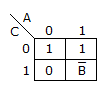
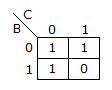
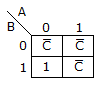
 m(0, 2, 4, 5, 6) can be represented by :
m(0, 2, 4, 5, 6) can be represented by : 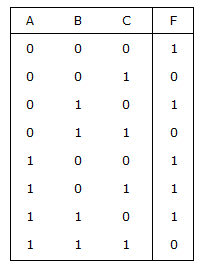
Now the Variable Entered Map (VEM) is:
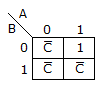
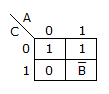
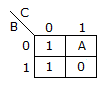
For proper recovery of signal |m(t)| ≤ 1.
f(x) = ex + e-x
f(x) = ex - ex
f(x) = 0 ⇒ ex - e-x = 0
f'(x) = ex + e-x ⇒ +ve for x = 0
Thus minimum.
Minimum f(x) = e0 + e0 = 2.
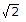 R1
R1