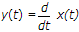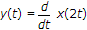Electronics and Communication Engineering - Exam Questions Papers
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 22
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 2
 are non zero, and one of its eigen values is zero. Which of the following statements is true?
are non zero, and one of its eigen values is zero. Which of the following statements is true?Use [λI - P] = 0
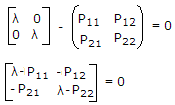
⇒(λ - P11)(λ - P22) - P21P12 = 0
Putting λ = 0, we get P11P22 - P21P12 = 0.
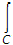 (4x3 + 10y4)
(4x3 + 10y4)
y = 2x
⇒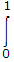 [4x3 + 10(2x)4]dx = 33
[4x3 + 10(2x)4]dx = 33
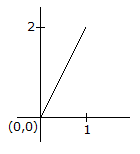

If θ1 = 2 rad. clockwise and the torque of gear 1 is 10 lb-ft, what is the displacement and torque of gear 7.
Number of teeths on any gear is proportional to its radius,
i.e. 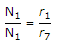
and also displacement on all gear must be same
=> r1θ1 = r7θ7
=> 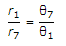
=> 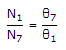
∴ 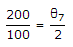
∴ 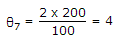 rad CW
rad CW
Now, work done by one gear is equal to other,
∴ T1θ1 = T7θ7
=> 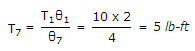 .
.
The system represented by expression ex(t) is static (memoryless) ∵ output at time = 't' dependent only.
In case of derivative, if we take the laplace transform we have to consider initial conditions.
Hence memory is required.
Now the problem can be solved using k-map method.
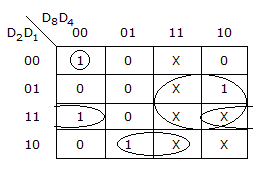
The function can be expressed as Σm(0, 3, 6, 9) + d(10, 11, 12, 13, 14, 15)
∴ K-map is
∴ The function is
D8D4D2D1 + D4D2D1 + D4D2D1 + D8D1 .
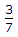 rad CW, 7.5 lb-ft
rad CW, 7.5 lb-ft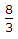 rad CW, 7.5 lb-ft
rad CW, 7.5 lb-ft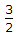 rad CW, 7.5 lb-ft
rad CW, 7.5 lb-ft