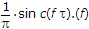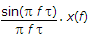IndiaBIX

Electronics and Communication Engineering - Exam Questions Papers

Exercise : Exam Questions Papers - Exam Paper 10
16.
A conductor in x-y plane and having length 1 m is moving with a velocity V = (2i + 3j + k) m/sec. A magnetic induction field B = (i + 2j) Wb/m2 is applied to the conductor. The potential difference between the ends of the conductor is
0
4.88 V
6 V
None of these
Answer: Option
Explanation:

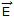= - (V x B) = - (2i + 3j + k) x (i + 2j)

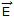∴ || = (E2x + E2y + E2z) = 6 v/m

∴ Potential Difference across 1 m length = 6.

17.
A 1000 kHz carrier wave modulated 40% at 4000 Hz is applied to a resonant circuit tuned to a carrier frequency and having Q = 140. What is the degree of modulation after passing the wave through this circuit?
0.4
0.2
0.27
0.554
Answer: Option
Explanation:

Resulting depth of modulation is given by :

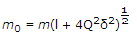
when δ =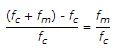

fc = 1000 x 103 Hz

fm = 4 x 103 Hz

δ =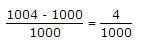

m0 =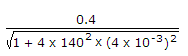

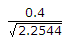= = 0.27 .

18.
The VTH at terminals A and B is equal to,
0 V
5 V
- 5 V
None of these
Answer: Option
Explanation:

Apply KVL to loop 1

5V - 3I1 - 2(I1 - I2) - 5V = 0

∴ I2 = 0

5 - 3I1 - 2I1 - 5V = 0

∴ I1 = 0

∴ VAB = 5V.

19.
If , then y has a
maximum at x = e
minimum at x = e
maximum at x = e-1
minimum at x = e-l
Answer: Option
Explanation:

.

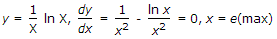20.
If . dt, then F[y(t)] is
- jsgn(f). x(f)
j2pf . e-jptf . x(f)
Answer: Option
Explanation:

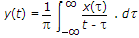
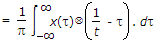
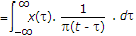
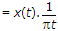
⇒ F{Y(t)} = Y(f) = X(f) x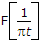

sin (t) ⇌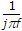

By duality :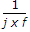⇌ sgn + (- f)

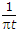⇒ ⇌ jsgn (- f)

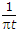∴⇌ - j sgn (f)

∵ sgn(- f) = - sgn(f)

⇒ Y(f) = X(f). [- j sgn(f)].

Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers