IndiaBIX

Electronics and Communication Engineering - Exam Questions Papers

Exercise : Exam Questions Papers - Exam Paper 9
41.
Given L[f(t)] = and L[g(t)] = also h(t) = , where, x = then, L[h(t)] = __________ .
Answer: Option
Explanation:

Now, x =

∴ log x = ejp x log S log x = y,

x = ey

log x = log Sejp

x = Sejp

x = S-1

∴

∴

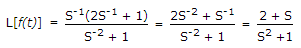
∴ L[f(t)] = L[f(t)] x L[g(t)].

42.
The voltage reflection coefficient on a 50 Ω line is 0.7∠30°.
The load impedance is
Answer: Option
Explanation:

.

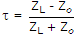43.
For finding the square root of N using Newton's iterative formula, the correct expression is:
Answer: Option
Explanation:

f(xn) = (x2n - N).

44.
For a random variable x following the probability density function, p(x), shown in figure, the mean and the variance are respectively,
1/2 and 2/3
1 and 4/3
1 and 2/3
2 and 4/3
Answer: Option
Explanation:

The mean x is given by

and the variance is

45.
VR at t < T, t = ∞
500e-40x104t, 0
100e-40x103t, 0
100e-40x106t, 0
100e-40x104t, 0
Answer: Option
Explanation:

At t = 0, C1, C2, C3 acts as short.

∴ entire voltage will appear cross R.

At t increases the voltage across the resistance decrease exponentially.

T = RCnet = 10 x 2.5 x 10-6 = 25 μ sec

Initial voltage

VR = V0e-t/RC at t = 0 = 100

= 100 e-t/25x10-6 V.

VR = 100 e-40x104t V.

At t = ∞, VR = 0

The charge C0 will be distributed in C1, C2, C3 and no current will flow.

Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers