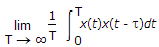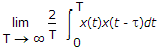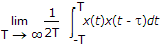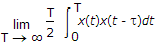Electronics and Communication Engineering - Exam Questions Papers
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 22
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 2
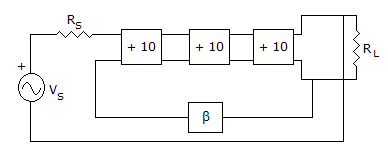
If the closed loop gain of above amplifier is + 100, the value of β will be
The T.F. 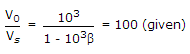
103 = 100 - 103 x 100 x β
900 = - 100000 x β
∴ β = - 9 x 10-3.
For signal x(- t) to be causal, the original signal x(t) has to be anticausal.
Similarly for signal x(- t) to be non causal, the original signal x(t) has to be causal.
Hence response of x(t) depends solely on x(t) only.
The expectations or ensemble average of a random process x(t) are averages "across the process".
The DC value of x(t) is defined by the time average
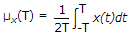
The other time average of particular interest is the autocorrelation function Rx(t, T) defined in terms of the sample function x(t) observed over the interval - T ≤ t ≤ T.
Following equation, we may formally define the time-averaged autocorrelation function of a sample function x(t) as follows :
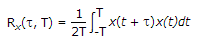
This second time-average should also be viewed as a random variable with a mean and variance of its own.
In a manner similar to ergodicity of the mean, we say that the process x(t) is ergodic in the autocorrelation function if the following two limiting conditions are satisfied :
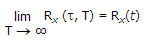
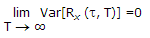 .
.
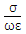 = 1 can be considered as the dividing line between the conductor and dielectrics for a good conductor
= 1 can be considered as the dividing line between the conductor and dielectrics for a good conductor 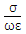 >> 1 and for good dielectrics
>> 1 and for good dielectrics 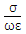 << 1 at any frequency ω.
<< 1 at any frequency ω.
Since for SR flip-flop all zero state is lock-in state; from which SR can not get out, the maximum length of sequence with 'n' bits will be 2n - 1.