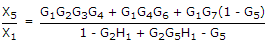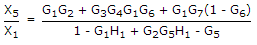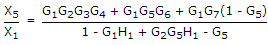Electronics and Communication Engineering - Exam Questions Papers
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 22
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 2
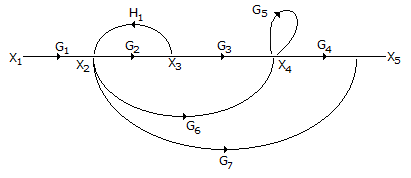
Number of forward paths K = 3
T1 = G1G2G3G4
T2 = G1G6G4
T3 = G1G7
Number of loops
L1 = G2H1
L2= G5
Δ = 1 - [L1 + L2] + [L1 L2]
= 1 - [G2H1 + G5] + [G2G5H1]
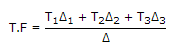
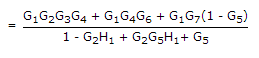 .
.
- Maximum energy of electrons liberated photoelectrically is independent of light intensity
- Maximum energy of electrons liberated photoelectrically varies nonlinearly with frequency of incident light.
Statement 2 is false because maximum energy of photons varies linearly with frequency of incident light. It can be shown as follows
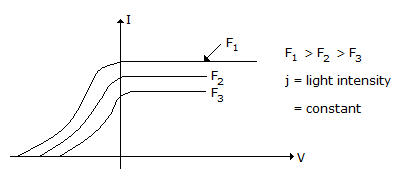
Photocurrent Vs Anode voltage with frequency and incident light as parameter the light intensity is constant.
F[x(t)] = X(f)
X(f) = 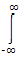 x(t).e- jpft.dt
x(t).e- jpft.dt
From above expression, the unit of x(t) x e-j2pft is volts and that of dt is seconds.
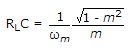
At f = 1 KHz
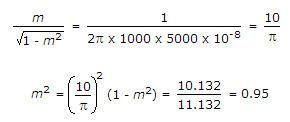
Similarly for 10 kHz,
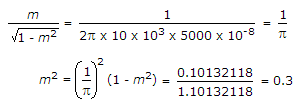
The ampere's law is given as
∇.H = J
Taking divergence on both sides
∇.(∇xH) = ∇.J
i.e., ∇.(∇xH) = ∇.J = 0
∴ divergence of curl is always zero
But ∇.J = -rv ... continuity equation.
Hence the inconsistency. It can be removed as follows
→
Let ∇ x H = J + G where G is some unknown quality.
Then ∇.(∇ x H) = ∇.(J x G) = 0
i.e. ∇.J + ∇.G = 0
i.e. ∇.J = -∇.G
or ∇.G = (-rv)
i.e. ∇.G = rv ...... Gauss's law in point form
Differentiating on both sides.
∇.D = rv
Comparing (i) and (ii), G = D
Thus ∇ x H = J + D
Where J is conduction current density and D is displacement current density which is added to remove the inconsistency of Ampere's law.