Electronics and Communication Engineering - Exam Questions Papers
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 22
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 2
Given, 137 + 276 = 435
Adding units digits i.e., 7 + 6 = 13, but given as 5, which is 13 - 8 and also 1 is carry forwarded to the tens digit.
i.e., + 1
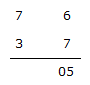
Here, 7 + 3 + 1 = 1 i.e., 11 - 8 = 3 and 1 is carry forwarded to hundred digits
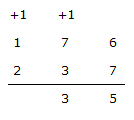
Now, the sum of digits in hundred's place is 1 + 1 + 2 = 4
ie.,
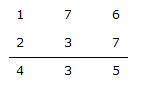
Using the same logic, we have
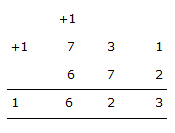
Using digits sum 1 + 2 = 3
Tens digits sum = 3 + 7 = 10
i.e., 10 - 2 and + 1 carry forward Hundreds digits sum = 1 + 7 + 6 = 14
i.e., 14 - 8 = 6 and one carry forward.
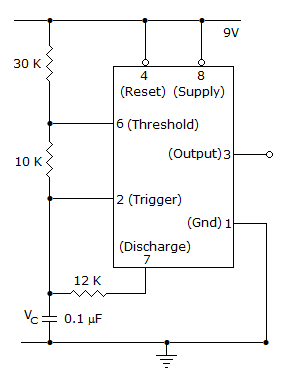
The voltage Vc across capacitor varies between
Charging and discharging level of capacitor will be the voltage across it.
This is equal to 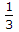 Vcc and
Vcc and 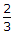 Vcc.
Vcc.
Thus 3V to 6V is the voltage VC across the capacitor.
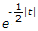 is
isConsider general expression
X(jω) = 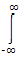 ea|t| e- jωt dt
ea|t| e- jωt dt
= 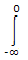 eat e-jωt dt +
eat e-jωt dt + 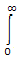 e-ate-jωt dt
e-ate-jωt dt
X(jω) = 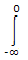 e(a - jω)t dt +
e(a - jω)t dt + 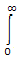 e -(a + jω)t dt
e -(a + jω)t dt
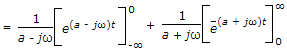
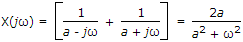
Since 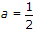 ∴
∴ 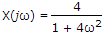 .
.
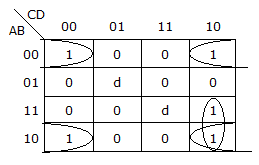
Y = A B D + A B D + A C D.
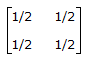 then |A50| will be
then |A50| will beAn = ?
Every n x n matrix satisfy its characteristic equation |A - λI| = 0 λ -> eigen vector
A - λI = 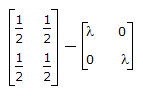
|A - λI| = 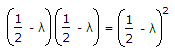 = 0
= 0
∴ 1 =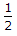 ,
, 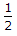
∴ f(A) = An = β0I + β1A
Replace A by 1, I by 1
f(λ) = λn = β0 + β1λ
Differentiate w.r.t. λ nλn - 1 = β1
β1 = 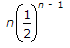
∴ β0 = λn - β x λ
β1 = 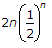
β0 = 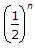 -
-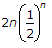
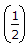 =
= 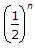 [1 - n]
[1 - n]
∴ An = 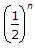 [1 - n]
[1 - n]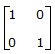 +
+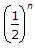 . 2n
. 2n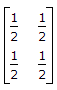
∴ An = 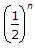
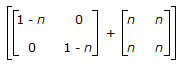
= 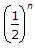
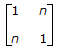
∴ A50 = 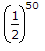
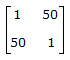
|A50| = 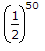 (1 - 502).
(1 - 502).
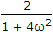
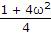
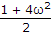
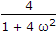
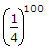 (1 - 1002)
(1 - 1002)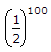 (1 - 1002)
(1 - 1002)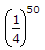 (1 - 502)
(1 - 502)