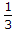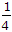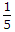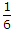Electronics and Communication Engineering - Exam Questions Papers
Exercise : Exam Questions Papers - Exam Paper 2
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 22
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 2
31.
If a signal f(t) has energy E, the energy of the signal f(2t) is equal to __________ .
Answer: Option
Explanation:
Energy content of a signal x(t), E = 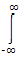 |f(t)|2 dt
|f(t)|2 dt
Now, E' = 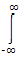 |f(2t)|2 dz for signal f(2t)
|f(2t)|2 dz for signal f(2t)
Putting 2t = z, we get
E' = 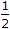
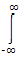 |f(t)|2 dz =
|f(t)|2 dz = 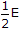 .
.
32.
For a npn BJT transistor fβ is 1.64 x 108 Hz. Cμ = 10-14 F; Cp = 4 x 10-13 F and DC current gain is 90. Find fT and gm (fβ = cut off frequency, Cμ = capacitance, Cp = parasitic capacitance, gm = transconductance, fT = gain BW product)
Answer: Option
Explanation:
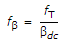
∴ fT = 90 x 1.64 x 108 = 1.47 x 1010 Hz
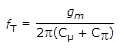
gm = 2pfT(Cμ + Cp) = 2 x p x 1.47 x 1010
= (10-14 + 4 x 10-13)
gm= 38 mμ.
33.
The impulse response h(t) of a linear time-invariant continuous time system is described by h(t) = exp (at) u(t) + exp (βt) u (- t), where u(t) denotes the unit step function, and a and β are constants. This system is stable if
Answer: Option
Explanation:
h(t) = e+atu(t) + eβtu(- t)
For h(t) to be stable h(t) dt < ∞
h(t) dt < ∞
It will happen when a is negative and β is positive.
34.
The probability density function of a random variable x is as shown.
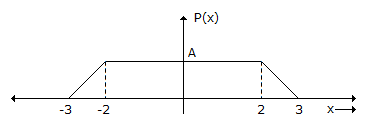
The value of A is:

The value of A is:
Answer: Option
Explanation:
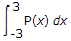 = 1
= 1
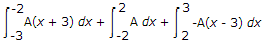 = 1
= 1
Solve this to get value of A = 1/5.
35.

ωL =
Answer: Option
Explanation:
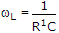
R1 = (10 + 10) = 20 kΩ
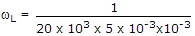
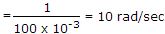 .
.
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers