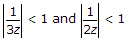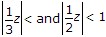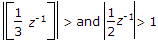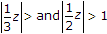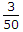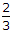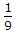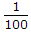Electronics and Communication Engineering - Exam Questions Papers
- Exam Questions Papers - Exam Paper 12
- Exam Questions Papers - Exam Paper 22
- Exam Questions Papers - Exam Paper 21
- Exam Questions Papers - Exam Paper 20
- Exam Questions Papers - Exam Paper 19
- Exam Questions Papers - Exam Paper 18
- Exam Questions Papers - Exam Paper 17
- Exam Questions Papers - Exam Paper 16
- Exam Questions Papers - Exam Paper 15
- Exam Questions Papers - Exam Paper 14
- Exam Questions Papers - Exam Paper 13
- Exam Questions Papers - Exam Paper 1
- Exam Questions Papers - Exam Paper 11
- Exam Questions Papers - Exam Paper 10
- Exam Questions Papers - Exam Paper 9
- Exam Questions Papers - Exam Paper 8
- Exam Questions Papers - Exam Paper 7
- Exam Questions Papers - Exam Paper 6
- Exam Questions Papers - Exam Paper 5
- Exam Questions Papers - Exam Paper 4
- Exam Questions Papers - Exam Paper 3
- Exam Questions Papers - Exam Paper 2
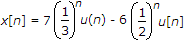 converges if and only if
converges if and only if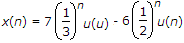
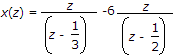
For u(n), a right handled sequence,
|z| > 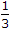 , |z| =
, |z| = 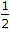
∴ |3z| > 1; |2z| > 1
∴ 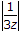 < 1;
< 1; 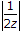 < 1.
< 1.
1 + G(s) H(s) = 0
s2 + 2s + 2 = 0
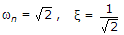
ξ < 1, under damped.
The given digits are 2, 2, 3, 3, 3, 4, 4, 4, 4 we have to find the numbers that are greater than 300
∴ The first digit can be 3 or 4 but not 2.
Now, let us fix the first, second and third digits as 3, 2, 2, then the fourth place can be filled in 3 ways.

∴ The number of ways is 3 similarly, we fix first third and fourth place as 3, 2 and 2 respectively (4) so the second place can be filled in 3 ways again,

The number of ways is 3
Now, we fix first, second and fourth, previous cases and we obtain the same result.
∴ The number of ways is 3 so, the total number of ways is 9 similarly this can done by fixing the numbers as 3 and 4 (instead of 2) and thereby we obtain the a ways each
The number of numbers starting with 3 is 27
Similarly by taking 4 as the first digit we get 27 numbers
∴ The number of numbers that are greater than 3000 is 27 + 27 = 54
But, 3222, 4222, is not possible as there are only two 2's, 3333 is not possible as there are only three 3's
∴ The total number of numbers that are greater than 3000 is 54 - 3 = 51.
- f1 =
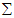 (2, 6, 11, 12)
(2, 6, 11, 12) - f2 =
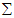 (2, 5, 14)
(2, 5, 14) 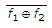 = p(2, 3, 4, 5, 9, 13, 14)
= p(2, 3, 4, 5, 9, 13, 14)
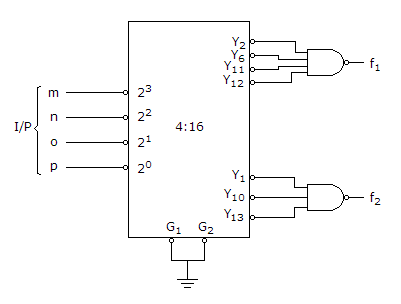
f1 = y2 + y6 + y11 + y12
and f2 = y1 + yl0 + yl3
f1(m, n, o, p) = 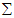 (3, 4, 9, 13)
(3, 4, 9, 13)
f2(m, n, o, p) = 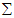 (2, 5, 14)
(2, 5, 14)
∴ 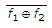 = Π(2, 3, 4, 5, 9, 13, 14).
= Π(2, 3, 4, 5, 9, 13, 14).
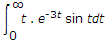 is
isCompare this with
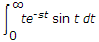 where s = 3.
where s = 3.