Electronics and Communication Engineering - Digital Electronics - Discussion
Discussion Forum : Digital Electronics - Section 1 (Q.No. 31)
31.
Minimum number of 2-input NAND gates required to implement the function F = (x + y) (Z + W) is
Answer: Option
Explanation:
F = (x + y) (z + w) = xy.(z + w)
= xyz + xyw
= 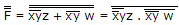 minimum no. of 2 input NAND gate.
minimum no. of 2 input NAND gate.
Discussion:
14 comments Page 1 of 2.
Harshita Sharma said:
6 years ago
F=(x'+y').(Z+W)
F=(xy)'.(Z+W)
F=(xy)'Z + (xy)'W
NAND GATE 1:
INPUT 1 = x
INPUT 2 = y
OUTPUT = (xy)'
Take this output as K => [K = (xy)']
NAND GATE 2:
INPUT 1 = Z
INPUT 2 = K
OUTPUT = [(xy)'z]'
Take this output as L => L= [(xy)'z]'
NAND GATE 3:
INPUT 1 = W
INPUT 2 = K
OUTPUT = [(xy)'W]'
Take this output as M => M = [(xy)'W]'
NAND GATE 4:
INPUT 1 = L
INPUT 2 = M
OUTPUT = [ ((xy)'W)' . ((xy)'Z)' ]'
Using De Morgan's Law
(A.B)' = A' + B'
(A + B)' = (A)' . (B)'
OUTPUT = { [(xy)'W]' }' + { [(xy)'Z]' }'
OUTPUT = (xy)'W + (xy)'Z
This output is equal to F = (xy)'Z + (xy)'W
I Hope, this solution will give clarity
F=(xy)'.(Z+W)
F=(xy)'Z + (xy)'W
NAND GATE 1:
INPUT 1 = x
INPUT 2 = y
OUTPUT = (xy)'
Take this output as K => [K = (xy)']
NAND GATE 2:
INPUT 1 = Z
INPUT 2 = K
OUTPUT = [(xy)'z]'
Take this output as L => L= [(xy)'z]'
NAND GATE 3:
INPUT 1 = W
INPUT 2 = K
OUTPUT = [(xy)'W]'
Take this output as M => M = [(xy)'W]'
NAND GATE 4:
INPUT 1 = L
INPUT 2 = M
OUTPUT = [ ((xy)'W)' . ((xy)'Z)' ]'
Using De Morgan's Law
(A.B)' = A' + B'
(A + B)' = (A)' . (B)'
OUTPUT = { [(xy)'W]' }' + { [(xy)'Z]' }'
OUTPUT = (xy)'W + (xy)'Z
This output is equal to F = (xy)'Z + (xy)'W
I Hope, this solution will give clarity
(6)
Vishnu said:
5 years ago
As far as time is concerned u won't get that much time to solve this question here is the shortcut.
What is nand====(xy)'==x'+y'.
Sso here is shortcut==(x'+y')(w+z)=(xy)'(w'z')'==1nand for (xy)' + 1 nand for (w'z')' + 1 nand to convert z' to z +1 nand to convert w' to w as we r not alloweded to use not in the circuit.
Hope it helped you guys.
What is nand====(xy)'==x'+y'.
Sso here is shortcut==(x'+y')(w+z)=(xy)'(w'z')'==1nand for (xy)' + 1 nand for (w'z')' + 1 nand to convert z' to z +1 nand to convert w' to w as we r not alloweded to use not in the circuit.
Hope it helped you guys.
(3)
Shiavnjali said:
1 decade ago
Any one can explain in detail?
Mangesh said:
1 decade ago
Why are we taking double bar?
Kruthi said:
10 years ago
We can replace 1 with double bar.
Riya said:
10 years ago
To get the simplified expression in terms of product form we take double bar on both sides.(the double bar doesn't change the value i.e.,F''=F)
If,
F'' = ((X' + Y')(Z = W))'',
F = (X'Z + X'W + Y'Z + Y'W)'',
F = ((X' + Y')' + (Z + W)')',
F = (X Y + Z'W')',
F = (X Y)' (Z + W,
F = (X Y)'Z + (X Y)'W.
By using four NAND gate we can implement the final expression.
If,
F'' = ((X' + Y')(Z = W))'',
F = (X'Z + X'W + Y'Z + Y'W)'',
F = ((X' + Y')' + (Z + W)')',
F = (X Y + Z'W')',
F = (X Y)' (Z + W,
F = (X Y)'Z + (X Y)'W.
By using four NAND gate we can implement the final expression.
Gaurang said:
9 years ago
Use DOT conversion rule, so we can convert F = (x' + y') (z + w) = xy + z'w'.
Now implement this using two input NAND gates.
Note: Use NAND as inverter to get z' and w'
The answer should be 5.
Now implement this using two input NAND gates.
Note: Use NAND as inverter to get z' and w'
The answer should be 5.
Tulasiram said:
9 years ago
(x'+y')(z+w)--->xor gate. 4 nand gates are required.
Jbel said:
9 years ago
(x' + y') (z + w) --- overall, AND function - to make NAND -> DOUBLE COMPLEMENT
{ [ (x' + y') (z + w) ]' }' -- then simplify terms in parenthesis: FACTOR OUT Negation (remember De Morgans).
{ [ (x y)' (z' w')' ]' }'
(xy)' - 1 NAND
z' - 1 NAND (complementation: SHORT two inputs)
w' - 1 NAND (complementation: SHORT two inputs)
(z'w')' - 1 NAND
[ (x y)' (z' w')' ]' - 1 NAND for the overall gate (carries all operations)
{ [ (x y)' (z' w')' ]' }' - LAST NAND for complement, since original term has AND overall function.
Overall, 6 NAND gates.
Well, not including INVERTERS, that would be 4.
{ [ (x' + y') (z + w) ]' }' -- then simplify terms in parenthesis: FACTOR OUT Negation (remember De Morgans).
{ [ (x y)' (z' w')' ]' }'
(xy)' - 1 NAND
z' - 1 NAND (complementation: SHORT two inputs)
w' - 1 NAND (complementation: SHORT two inputs)
(z'w')' - 1 NAND
[ (x y)' (z' w')' ]' - 1 NAND for the overall gate (carries all operations)
{ [ (x y)' (z' w')' ]' }' - LAST NAND for complement, since original term has AND overall function.
Overall, 6 NAND gates.
Well, not including INVERTERS, that would be 4.
Jagannath said:
9 years ago
F=(x'+y')(w+z)=(xy)'(w+z) now 1st take a NAND gate with the input X,Y that will produce (xy)'=k.
Let assume then take another two NAND gate which inputs are K ,W and K,Z then take another NAND gate with the input of those outputs that will produce the desire output.
Let assume then take another two NAND gate which inputs are K ,W and K,Z then take another NAND gate with the input of those outputs that will produce the desire output.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers