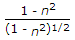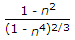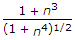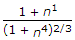Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 1 (Q.No. 24)
24.
If n is the ratio of internal and external diameters of a hollow shaft, the ratio of the weight of the hollow shaft and that of solid shaft of same strength, will be
Discussion:
15 comments Page 1 of 2.
M.raja reddy(svkp cumbum) said:
10 years ago
Anyone give explanation for the answer.
Dalisha said:
9 years ago
Given, d/D = n and stress ratio D^4 - d^4/D^4 = Th/Ts.
Now, d = nD, D = d/n putin above and get 1 - n^2/(1 - n^4)^2/3.
Now, d = nD, D = d/n putin above and get 1 - n^2/(1 - n^4)^2/3.
Ram Krishna Adhikari said:
9 years ago
Now, d = nD, D = d/n.
Ratio of the weight = ratio of C/A = (d^2 * (1/n^2-1))/D^2 ...1.
Find d^/D^2 as follows:
((d/n)^3 - d^3)/D^3 = Th/Ts = 1
(d/D)^2 = (1-n^2)/(1-n^4)^(2/3).
Substitute in eq 1 you will get the answer.
Ratio of the weight = ratio of C/A = (d^2 * (1/n^2-1))/D^2 ...1.
Find d^/D^2 as follows:
((d/n)^3 - d^3)/D^3 = Th/Ts = 1
(d/D)^2 = (1-n^2)/(1-n^4)^(2/3).
Substitute in eq 1 you will get the answer.
Tailam mahesh said:
9 years ago
I can't understand. Can anyone explain clearly?
LATHA said:
8 years ago
Please expain clearly.
Prasenjit said:
8 years ago
Explain it please.
Krishna sai said:
8 years ago
Assume External diameter = d then internal diameter = nd.
As both the cases have equal strength so equate both strength which is polar modulus
case 1 polar modulus = pi()*(d^4-nd^4)/32/d/2
case 2 polar modulus = pi()*(D^3)/16.
Equating both find D in terms of n pi()*(d^4-nd^4)/32/d/2 = pi()*(D^3)/16
D = d((1-n^4)^1/3.
Now weight is directly proportional to Area.
area in case 1 = pi()*(d^2-nd^2)/4,
Area in case 2 = PI()*(d((1-n^4)^1/3)^2/4,
dividing both we get the ratio as (1-n^2)/(1-n^4)^2/3.
As both the cases have equal strength so equate both strength which is polar modulus
case 1 polar modulus = pi()*(d^4-nd^4)/32/d/2
case 2 polar modulus = pi()*(D^3)/16.
Equating both find D in terms of n pi()*(d^4-nd^4)/32/d/2 = pi()*(D^3)/16
D = d((1-n^4)^1/3.
Now weight is directly proportional to Area.
area in case 1 = pi()*(d^2-nd^2)/4,
Area in case 2 = PI()*(d((1-n^4)^1/3)^2/4,
dividing both we get the ratio as (1-n^2)/(1-n^4)^2/3.
Thakur said:
8 years ago
Thanks @Krishna.
Sheela said:
8 years ago
Thanks @Krishna.
Vikas kumar said:
7 years ago
What is polar modulus?
And what is p=, I=?
And what is p=, I=?
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers