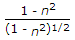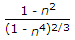Civil Engineering - Strength of Materials - Discussion
Discussion Forum : Strength of Materials - Section 1 (Q.No. 24)
24.
If n is the ratio of internal and external diameters of a hollow shaft, the ratio of the weight of the hollow shaft and that of solid shaft of same strength, will be
Discussion:
15 comments Page 1 of 2.
Vivek said:
4 years ago
Thank you @Krishna.
Anvesh said:
5 years ago
Thank you @Krishna.
Manvitha said:
6 years ago
Thank you @Krishna.
U.S.lakshmi said:
6 years ago
I am going to prepare with this help after second carrying after two years so please explain with notations and clearly.
Shankar said:
7 years ago
The strength of shaft means max. torque or max power transmitted capacity.
Here asking their strength equal means weight ratio of the shaft.
So weight depends on the size of the shaft.
We taking maximum torque equation of finding dia of the shaft.
Consider d for outer dia of hollow shaft and nd for inner dia of the shaft.
Then formula = (π) * [ d^4 - (nd)^4] * shear stress /16/d^4.
Assume dia of solid shaft D.
Then we equating torque of solid shaft = torque of the hollow shaft
we get D = { [d^4 - (nd)^4 ]/ d^4 }
The weight depends on the area of the shaft section so,
Hollow shaft cross-section area / solid shaft cross-section area.
By substituting the value of solid shaft dia in area formula we get the final answer.
Here asking their strength equal means weight ratio of the shaft.
So weight depends on the size of the shaft.
We taking maximum torque equation of finding dia of the shaft.
Consider d for outer dia of hollow shaft and nd for inner dia of the shaft.
Then formula = (π) * [ d^4 - (nd)^4] * shear stress /16/d^4.
Assume dia of solid shaft D.
Then we equating torque of solid shaft = torque of the hollow shaft
we get D = { [d^4 - (nd)^4 ]/ d^4 }
The weight depends on the area of the shaft section so,
Hollow shaft cross-section area / solid shaft cross-section area.
By substituting the value of solid shaft dia in area formula we get the final answer.
Vikas kumar said:
7 years ago
What is polar modulus?
And what is p=, I=?
And what is p=, I=?
Sheela said:
8 years ago
Thanks @Krishna.
Thakur said:
8 years ago
Thanks @Krishna.
Krishna sai said:
8 years ago
Assume External diameter = d then internal diameter = nd.
As both the cases have equal strength so equate both strength which is polar modulus
case 1 polar modulus = pi()*(d^4-nd^4)/32/d/2
case 2 polar modulus = pi()*(D^3)/16.
Equating both find D in terms of n pi()*(d^4-nd^4)/32/d/2 = pi()*(D^3)/16
D = d((1-n^4)^1/3.
Now weight is directly proportional to Area.
area in case 1 = pi()*(d^2-nd^2)/4,
Area in case 2 = PI()*(d((1-n^4)^1/3)^2/4,
dividing both we get the ratio as (1-n^2)/(1-n^4)^2/3.
As both the cases have equal strength so equate both strength which is polar modulus
case 1 polar modulus = pi()*(d^4-nd^4)/32/d/2
case 2 polar modulus = pi()*(D^3)/16.
Equating both find D in terms of n pi()*(d^4-nd^4)/32/d/2 = pi()*(D^3)/16
D = d((1-n^4)^1/3.
Now weight is directly proportional to Area.
area in case 1 = pi()*(d^2-nd^2)/4,
Area in case 2 = PI()*(d((1-n^4)^1/3)^2/4,
dividing both we get the ratio as (1-n^2)/(1-n^4)^2/3.
Prasenjit said:
8 years ago
Explain it please.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers