Aptitude - Problems on Trains - Discussion
Discussion Forum : Problems on Trains - General Questions (Q.No. 27)
27.
A train overtakes two persons who are walking in the same direction in which the train is going, at the rate of 2 kmph and 4 kmph and passes them completely in 9 and 10 seconds respectively. The length of the train is:
Answer: Option
Explanation:
| 2 kmph = |  |
2 x | 5 |  |
m/sec = | 5 | m/sec. |
| 18 | 9 |
| 4 kmph = |  |
4 x | 5 |  |
m/sec = | 10 | m/sec. |
| 18 | 9 |
Let the length of the train be x metres and its speed by y m/sec.
| Then, | 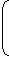 |
x |  |
= 9 and | 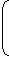 |
x |  |
= 10. |
|
|
 9y - 5 = x and 10(9y - 10) = 9x
9y - 5 = x and 10(9y - 10) = 9x
 9y - x = 5 and 90y - 9x = 100.
9y - x = 5 and 90y - 9x = 100.
On solving, we get: x = 50.
 Length of the train is 50 m.
Length of the train is 50 m.
Discussion:
108 comments Page 1 of 11.
Nandini said:
2 months ago
I think we should add only the train length + the stationary object length according to the formula, man is not under a stationary object.
That's why the 2 travel distances are not added.
That's why the 2 travel distances are not added.
Sujeet said:
3 months ago
Since both the person are moving.
They two will travel some distance + the length of the train.
Then why only take the length of the train? Please explain to me.
They two will travel some distance + the length of the train.
Then why only take the length of the train? Please explain to me.
Vivek Tiwari said:
4 months ago
@All.
Just, let the length of train = x, then find the speed of the train after that equals the relative speed of person and the relative sped of the train.
Just, let the length of train = x, then find the speed of the train after that equals the relative speed of person and the relative sped of the train.
Karanam Sai Charan said:
9 months ago
Use this formulae:
L = ((T1*T2)/T2-T1) * ( S2 - S1),
= ((9*10)/10-9) * (4-2),
= 90 * 2(5/18),
= 50.4 or 50.
L = ((T1*T2)/T2-T1) * ( S2 - S1),
= ((9*10)/10-9) * (4-2),
= 90 * 2(5/18),
= 50.4 or 50.
(3)
Pavi said:
1 year ago
The speed is already given in that question itself so why do you declare that as y?
(3)
Hellen said:
1 year ago
Certainly! Here’s a simplified step-by-step process to find the length of the train without getting into complex details:
Given:
• Person 1’s Speed: 2 km/h (overtakes in 9 seconds)
• Person 2’s Speed: 4 km/h (overtakes in 10 seconds)
Steps to Calculate Length of the Train:
1. Convert Speeds from km/h to m/s:
• Person 1’s Speed:
• Person 2’s Speed:
2. Calculate Relative Speed:
• Let be the speed of the train in m/s.
• Relative speed with respect to Person 1:
• Relative speed with respect to Person 2:
3. Use the Length Formula:
• Length of the train when overtaking Person 1 (in 9 seconds):
• Length of the train when overtaking Person 2 (in 10 seconds):
4. Set the Two Lengths Equal:
Since both expressions equal the length of the train:
5. Solve for
• Expand and rearrange the equation:
6. Calculate the Length of the Train:
Substitute back into either length formula. Using the first person:
Final Result:
The length of the train is approximately 50 meters.
Summary of Steps:
1. Convert speeds to m/s.
2. Set up equations for lengths based on relative speed.
3. Set the equations equal to find the speed of the train.
4. Substitute back to find the length.
This streamlined process makes it easier to follow and calculate the length of the train. Let me know if you need any more simplifications!
Given:
• Person 1’s Speed: 2 km/h (overtakes in 9 seconds)
• Person 2’s Speed: 4 km/h (overtakes in 10 seconds)
Steps to Calculate Length of the Train:
1. Convert Speeds from km/h to m/s:
• Person 1’s Speed:
• Person 2’s Speed:
2. Calculate Relative Speed:
• Let be the speed of the train in m/s.
• Relative speed with respect to Person 1:
• Relative speed with respect to Person 2:
3. Use the Length Formula:
• Length of the train when overtaking Person 1 (in 9 seconds):
• Length of the train when overtaking Person 2 (in 10 seconds):
4. Set the Two Lengths Equal:
Since both expressions equal the length of the train:
5. Solve for
• Expand and rearrange the equation:
6. Calculate the Length of the Train:
Substitute back into either length formula. Using the first person:
Final Result:
The length of the train is approximately 50 meters.
Summary of Steps:
1. Convert speeds to m/s.
2. Set up equations for lengths based on relative speed.
3. Set the equations equal to find the speed of the train.
4. Substitute back to find the length.
This streamlined process makes it easier to follow and calculate the length of the train. Let me know if you need any more simplifications!
(2)
Prachi rokade said:
3 years ago
Can solve this way: Same direction a person walk so the subtraction of speed i.e 4-2 = 2kmph.
And (2*5/18)m/s =5/9.
Now the time is 9 and 10-sec addition of two is 90.
So, 90 * 5/9 = 50.
And (2*5/18)m/s =5/9.
Now the time is 9 and 10-sec addition of two is 90.
So, 90 * 5/9 = 50.
(34)
Chandini said:
3 years ago
Why we multiply 9 and 10 here? can anyone explain?
(23)
Sidd said:
3 years ago
How? please anyone explain me.
(3)
GURU CHARAN MUNDA said:
3 years ago
Good, Thanks @Anushree.
(1)
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers