Aptitude - Problems on Trains - Discussion
Discussion Forum : Problems on Trains - General Questions (Q.No. 27)
27.
A train overtakes two persons who are walking in the same direction in which the train is going, at the rate of 2 kmph and 4 kmph and passes them completely in 9 and 10 seconds respectively. The length of the train is:
Answer: Option
Explanation:
| 2 kmph = |  |
2 x | 5 |  |
m/sec = | 5 | m/sec. |
| 18 | 9 |
| 4 kmph = | |
4 x | 5 | |
m/sec = | 10 | m/sec. |
| 18 | 9 |
Let the length of the train be x metres and its speed by y m/sec.
| Then, |  |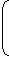
x |  |
= 9 and | |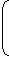
x | |
= 10. |
|
|
9y - 5 = x and 10(9y - 10) = 9x
9y - x = 5 and 90y - 9x = 100.
On solving, we get: x = 50.
Length of the train is 50 m.
Discussion:
106 comments Page 1 of 11.
Sasikumar said:
2 decades ago
Why 5/9 is subtracted with y? Please any one tell the answer.
Gopal said:
1 decade ago
Here man walking same direction of train because.
Relitive speed = train speed - man spped.
Ok.
Relitive speed = train speed - man spped.
Ok.
Kapil said:
1 decade ago
Let train speed be s
1st person's speed,s1 = 2km/hr =2*(5/18)=5/9 m/sec
2nd person's speed,s2 = 4km/h = 4*(5/18)=10/9 m/sec
Length of train,d = (s-s1)*t1 or (s-s2)*t2
so, (s-5/9)* 9 = (s-10/9)* 10 [t1=9sec, t2=10sec]
s=55/9 sec
Now,take 1st eq.
s-s1= d/t1 [bcz, Speed=Dis/Time]
(55/11)-(5/9)=d/9
Therefore we get d(length of train)=50m
1st person's speed,s1 = 2km/hr =2*(5/18)=5/9 m/sec
2nd person's speed,s2 = 4km/h = 4*(5/18)=10/9 m/sec
Length of train,d = (s-s1)*t1 or (s-s2)*t2
so, (s-5/9)* 9 = (s-10/9)* 10 [t1=9sec, t2=10sec]
s=55/9 sec
Now,take 1st eq.
s-s1= d/t1 [bcz, Speed=Dis/Time]
(55/11)-(5/9)=d/9
Therefore we get d(length of train)=50m
Nayana said:
1 decade ago
Here after solving 10=x/9y-10 will give rise 90y-100=x.
After solving 9=x/9y-5 we are getting 9y-5=x. here why we they are not multiplying 9 with (9y-5).
Please any tell the answer for this.
After solving 9=x/9y-5 we are getting 9y-5=x. here why we they are not multiplying 9 with (9y-5).
Please any tell the answer for this.
Ranu said:
1 decade ago
See
9=(x/y-5/9)
when we solve dis..the LCM comes as 9 which get cancelled by 9 on the other side of the equation.
x*9/9y-5=9
9x=9(9y-5)
x=9y-5
But in case of 10=x/y-10/9, the LCM 9 is not cancelled with 10 on the other side & thus
x*9/9y-10=10
9x=10(9y-10)
9x=90y-100
9=(x/y-5/9)
when we solve dis..the LCM comes as 9 which get cancelled by 9 on the other side of the equation.
x*9/9y-5=9
9x=9(9y-5)
x=9y-5
But in case of 10=x/y-10/9, the LCM 9 is not cancelled with 10 on the other side & thus
x*9/9y-10=10
9x=10(9y-10)
9x=90y-100
Nayana said:
1 decade ago
@ Ranu
Hi Ranu,
Thank you so much
Hi Ranu,
Thank you so much
Md Ali Umar said:
1 decade ago
@Kapil
You solved the problem in very easily. I agree with it but finally you got speed 55/9 sec. It is not correct the unit of speed. The unit of speed in SI is m/s.
You solved the problem in very easily. I agree with it but finally you got speed 55/9 sec. It is not correct the unit of speed. The unit of speed in SI is m/s.
Nikita said:
1 decade ago
Let consider the speed of train is x;
then distance is constant.
So
9*(5/9-x)=10*(10/9*x);
by solving
x=55/9
now length of train=
9*(5/9-55/9)
=50
(distance never be -ve)
then distance is constant.
So
9*(5/9-x)=10*(10/9*x);
by solving
x=55/9
now length of train=
9*(5/9-55/9)
=50
(distance never be -ve)
Vinay said:
1 decade ago
Kapil finally it is 55/9 not 55/11 ok, you had solved really great.
Syndhya said:
1 decade ago
@Kapil
Please say why we are taking here why here we taking s-s1 and not s-s2 in your solution.
Please say why we are taking here why here we taking s-s1 and not s-s2 in your solution.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers