Aptitude - Problems on Trains - Discussion
Discussion Forum : Problems on Trains - General Questions (Q.No. 27)
27.
A train overtakes two persons who are walking in the same direction in which the train is going, at the rate of 2 kmph and 4 kmph and passes them completely in 9 and 10 seconds respectively. The length of the train is:
Answer: Option
Explanation:
| 2 kmph = |  |
2 x | 5 |  |
m/sec = | 5 | m/sec. |
| 18 | 9 |
| 4 kmph = |  |
4 x | 5 |  |
m/sec = | 10 | m/sec. |
| 18 | 9 |
Let the length of the train be x metres and its speed by y m/sec.
| Then, | 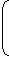 |
x |  |
= 9 and | 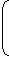 |
x |  |
= 10. |
|
|
 9y - 5 = x and 10(9y - 10) = 9x
9y - 5 = x and 10(9y - 10) = 9x
 9y - x = 5 and 90y - 9x = 100.
9y - x = 5 and 90y - 9x = 100.
On solving, we get: x = 50.
 Length of the train is 50 m.
Length of the train is 50 m.
Discussion:
108 comments Page 1 of 11.
Hellen said:
1 year ago
Certainly! Here’s a simplified step-by-step process to find the length of the train without getting into complex details:
Given:
• Person 1’s Speed: 2 km/h (overtakes in 9 seconds)
• Person 2’s Speed: 4 km/h (overtakes in 10 seconds)
Steps to Calculate Length of the Train:
1. Convert Speeds from km/h to m/s:
• Person 1’s Speed:
• Person 2’s Speed:
2. Calculate Relative Speed:
• Let be the speed of the train in m/s.
• Relative speed with respect to Person 1:
• Relative speed with respect to Person 2:
3. Use the Length Formula:
• Length of the train when overtaking Person 1 (in 9 seconds):
• Length of the train when overtaking Person 2 (in 10 seconds):
4. Set the Two Lengths Equal:
Since both expressions equal the length of the train:
5. Solve for
• Expand and rearrange the equation:
6. Calculate the Length of the Train:
Substitute back into either length formula. Using the first person:
Final Result:
The length of the train is approximately 50 meters.
Summary of Steps:
1. Convert speeds to m/s.
2. Set up equations for lengths based on relative speed.
3. Set the equations equal to find the speed of the train.
4. Substitute back to find the length.
This streamlined process makes it easier to follow and calculate the length of the train. Let me know if you need any more simplifications!
Given:
• Person 1’s Speed: 2 km/h (overtakes in 9 seconds)
• Person 2’s Speed: 4 km/h (overtakes in 10 seconds)
Steps to Calculate Length of the Train:
1. Convert Speeds from km/h to m/s:
• Person 1’s Speed:
• Person 2’s Speed:
2. Calculate Relative Speed:
• Let be the speed of the train in m/s.
• Relative speed with respect to Person 1:
• Relative speed with respect to Person 2:
3. Use the Length Formula:
• Length of the train when overtaking Person 1 (in 9 seconds):
• Length of the train when overtaking Person 2 (in 10 seconds):
4. Set the Two Lengths Equal:
Since both expressions equal the length of the train:
5. Solve for
• Expand and rearrange the equation:
6. Calculate the Length of the Train:
Substitute back into either length formula. Using the first person:
Final Result:
The length of the train is approximately 50 meters.
Summary of Steps:
1. Convert speeds to m/s.
2. Set up equations for lengths based on relative speed.
3. Set the equations equal to find the speed of the train.
4. Substitute back to find the length.
This streamlined process makes it easier to follow and calculate the length of the train. Let me know if you need any more simplifications!
(2)
Javid Mir said:
1 decade ago
There are two cases:
In the first case, speed of man = 2 km/h => 2x5/18 => 5/9 m/sec.
Therefore, relative speed of train we know that first train (let speed of train be 'V') ,
V-5/9 = L/9....(1) here 'L' is length of train.
Now, for 2nd case, speed of man = 4 km/h => 4x5/18 => 10/9 m/sec.
Therefore, V-10/9 = L/10....(2).
From equation (1) we get,
9V-5/9 = L/9.
Cut denominator 9 on both side we get.
9V-5 = L or 9V = L+5 or V = (L+5) /9.
Now substituting the value of V in equation --- (2).
(L+5) /9 - 10/9 = L/10.
L+5-10/9 = L/10.
L+5-10 = 9L/10.
On cross multiplication,
10L+50-100 = 9L.
On rearranging.
10L-9L = 100-50.
L = 50 meters.
In the first case, speed of man = 2 km/h => 2x5/18 => 5/9 m/sec.
Therefore, relative speed of train we know that first train (let speed of train be 'V') ,
V-5/9 = L/9....(1) here 'L' is length of train.
Now, for 2nd case, speed of man = 4 km/h => 4x5/18 => 10/9 m/sec.
Therefore, V-10/9 = L/10....(2).
From equation (1) we get,
9V-5/9 = L/9.
Cut denominator 9 on both side we get.
9V-5 = L or 9V = L+5 or V = (L+5) /9.
Now substituting the value of V in equation --- (2).
(L+5) /9 - 10/9 = L/10.
L+5-10/9 = L/10.
L+5-10 = 9L/10.
On cross multiplication,
10L+50-100 = 9L.
On rearranging.
10L-9L = 100-50.
L = 50 meters.
Talha said:
3 years ago
Hello everyone. Please have a look at my method of solution. It is giving a different answer.
Let,
the Speed of the train = x.
Then,
With respect to the first person;
The relative speed of the train = (x-2)*5/18 m/s.
Time is taken to cross the first person = 9s,
Length of the train = Speed * Time = (x-2)*(5/18)*9.
With respect to the second person;
The relative speed of the train = (x-4)*5/18 m/s.
Time is taken to cross the first person = 10s.
Length of the train = Speed * Time = (x-4)*(5/18)*10.
As both lengths are of the same body (train), so;
(x-2)*(5/18)*9 = (x-4)*(5/18)*10.
(x-2)*(5/2) = (x-4)*(25/9).
Upon solving, we get:
x = 22m.
Let,
the Speed of the train = x.
Then,
With respect to the first person;
The relative speed of the train = (x-2)*5/18 m/s.
Time is taken to cross the first person = 9s,
Length of the train = Speed * Time = (x-2)*(5/18)*9.
With respect to the second person;
The relative speed of the train = (x-4)*5/18 m/s.
Time is taken to cross the first person = 10s.
Length of the train = Speed * Time = (x-4)*(5/18)*10.
As both lengths are of the same body (train), so;
(x-2)*(5/18)*9 = (x-4)*(5/18)*10.
(x-2)*(5/2) = (x-4)*(25/9).
Upon solving, we get:
x = 22m.
(9)
Jayasree said:
5 years ago
Let me explain if anyone wants to know how to solve the value of x,
So we got both the equations ( 1,2 ) by solving (x/ y-5/9) = 9 and (x/ y-10/9) = 10,
9y - 5 = x ->(1) , 10(9y - 10) = 9x ->(2)
By substituting equation no (1) in equation no (2), we will get,
10(9y - 10) = 9(9y - 5),
90y - 100 = 81y - 45.
9y = 55.
| y = 55/9.
Now substitute the value of (y) in equation no (1) to get the value of (x)
9(55/9) - 5 = x.
55-5 = x.
x = 50.
Thank you.
So we got both the equations ( 1,2 ) by solving (x/ y-5/9) = 9 and (x/ y-10/9) = 10,
9y - 5 = x ->(1) , 10(9y - 10) = 9x ->(2)
By substituting equation no (1) in equation no (2), we will get,
10(9y - 10) = 9(9y - 5),
90y - 100 = 81y - 45.
9y = 55.
| y = 55/9.
Now substitute the value of (y) in equation no (1) to get the value of (x)
9(55/9) - 5 = x.
55-5 = x.
x = 50.
Thank you.
(9)
Mancy said:
1 decade ago
@everyone who didn't get how x= 50 came?
Let me explain in easy way.
Here, on solving we get,
9y-x = 5.........eq no.1.
&90y-9x = 100......eq no.2.
Now, take eq no.1.
9y-x = 5.
9y = 5+x.
y = 5+x/9.
Now put the value of y in eq no.2 then,
90y-9x = 100.
90(5+x/9)-9x = 100 ( here y= 5+x/9).
Now in L.H.S 90 is cancelled by 9 and become 10.
So, 10(5+x)-9x = 100.
50+10x-9x = 100.
50 +x = 100.
x = 100-50.
Answer x = 50.
Hope you'll get it now.
Let me explain in easy way.
Here, on solving we get,
9y-x = 5.........eq no.1.
&90y-9x = 100......eq no.2.
Now, take eq no.1.
9y-x = 5.
9y = 5+x.
y = 5+x/9.
Now put the value of y in eq no.2 then,
90y-9x = 100.
90(5+x/9)-9x = 100 ( here y= 5+x/9).
Now in L.H.S 90 is cancelled by 9 and become 10.
So, 10(5+x)-9x = 100.
50+10x-9x = 100.
50 +x = 100.
x = 100-50.
Answer x = 50.
Hope you'll get it now.
Amigo said:
5 years ago
Instead of taking 2 variables.
Step1 : Simply find the velocity of the train. If velocity is known we can find the distance, since time is already;
Given.
(x - 5/9)*9 = (x - 10/9)*10,
81x - 45 = 90x - 100,
==> x = 55/9.
Step2 : Since we know the time for each man, take anyone say the man with velocity 10/9.
Relative velocity = (55 -10)/9 = 5/9.
Step3 : Distance = relative vel * time.
x = 5*10/9 = 50m.
Thank you.
Step1 : Simply find the velocity of the train. If velocity is known we can find the distance, since time is already;
Given.
(x - 5/9)*9 = (x - 10/9)*10,
81x - 45 = 90x - 100,
==> x = 55/9.
Step2 : Since we know the time for each man, take anyone say the man with velocity 10/9.
Relative velocity = (55 -10)/9 = 5/9.
Step3 : Distance = relative vel * time.
x = 5*10/9 = 50m.
Thank you.
(1)
Ronie said:
7 years ago
You first solve for y which will give y=55/9m/s now convert it into km/h which will be 22km/h
But the actual speed of the train is:
(22-2)km/h=20km/h
2km/h is the speed of the 1st person
20km/h is 50/9 m/s when you convert
Now as we know,
Length of train = speed * time.
So, L=(50/9)*9,
or, L=50m.
Go through the formula how to convert kmph to mps. Because when it is given in seconds you have to convert it to mph.
But the actual speed of the train is:
(22-2)km/h=20km/h
2km/h is the speed of the 1st person
20km/h is 50/9 m/s when you convert
Now as we know,
Length of train = speed * time.
So, L=(50/9)*9,
or, L=50m.
Go through the formula how to convert kmph to mps. Because when it is given in seconds you have to convert it to mph.
Amit said:
1 decade ago
2km/hr = 5/9 m/s,,4km/hr = 10/9 m/s.
let speed=S m/s & lenth = L mtr.
Both man and train moving in same direction so speed of train w.r.to man will be (Speed of train-Speed of man).
case1: S-5/9 = L/9 (Speed=Distance/Time here Length is distance).
Case2: S-10/9 = L/10 (Time--- 9 & 10 sec given).
=>90S-50 = 10L & 90S-100 = 9L.
L = 50 m.
let speed=S m/s & lenth = L mtr.
Both man and train moving in same direction so speed of train w.r.to man will be (Speed of train-Speed of man).
case1: S-5/9 = L/9 (Speed=Distance/Time here Length is distance).
Case2: S-10/9 = L/10 (Time--- 9 & 10 sec given).
=>90S-50 = 10L & 90S-100 = 9L.
L = 50 m.
Anand K said:
5 years ago
Treat both people separately.
1st compare person A(2 kmph) and train.
Speed = dist/time.
hence time = dist/speed.
Time(for A) = 9s.
Dist = length of train
Speed = relative speed btw A and train=(S-5/9)
S = speed of the train.
9 = LOT/(S-5/9) //LOT=Length of train.
Apply same for person B.
10=LOT/(S-10/9).
solve both equations and get;
LOT= 50mtrs.
1st compare person A(2 kmph) and train.
Speed = dist/time.
hence time = dist/speed.
Time(for A) = 9s.
Dist = length of train
Speed = relative speed btw A and train=(S-5/9)
S = speed of the train.
9 = LOT/(S-5/9) //LOT=Length of train.
Apply same for person B.
10=LOT/(S-10/9).
solve both equations and get;
LOT= 50mtrs.
Kapil said:
2 decades ago
Let train speed be s
1st person's speed,s1 = 2km/hr =2*(5/18)=5/9 m/sec
2nd person's speed,s2 = 4km/h = 4*(5/18)=10/9 m/sec
Length of train,d = (s-s1)*t1 or (s-s2)*t2
so, (s-5/9)* 9 = (s-10/9)* 10 [t1=9sec, t2=10sec]
s=55/9 sec
Now,take 1st eq.
s-s1= d/t1 [bcz, Speed=Dis/Time]
(55/11)-(5/9)=d/9
Therefore we get d(length of train)=50m
1st person's speed,s1 = 2km/hr =2*(5/18)=5/9 m/sec
2nd person's speed,s2 = 4km/h = 4*(5/18)=10/9 m/sec
Length of train,d = (s-s1)*t1 or (s-s2)*t2
so, (s-5/9)* 9 = (s-10/9)* 10 [t1=9sec, t2=10sec]
s=55/9 sec
Now,take 1st eq.
s-s1= d/t1 [bcz, Speed=Dis/Time]
(55/11)-(5/9)=d/9
Therefore we get d(length of train)=50m
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers