Aptitude - Problems on Trains - Discussion
Discussion Forum : Problems on Trains - General Questions (Q.No. 27)
27.
A train overtakes two persons who are walking in the same direction in which the train is going, at the rate of 2 kmph and 4 kmph and passes them completely in 9 and 10 seconds respectively. The length of the train is:
Answer: Option
Explanation:
| 2 kmph = |  |
2 x | 5 |  |
m/sec = | 5 | m/sec. |
| 18 | 9 |
| 4 kmph = |  |
4 x | 5 |  |
m/sec = | 10 | m/sec. |
| 18 | 9 |
Let the length of the train be x metres and its speed by y m/sec.
| Then, | 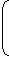 |
x |  |
= 9 and | 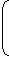 |
x |  |
= 10. |
|
|
 9y - 5 = x and 10(9y - 10) = 9x
9y - 5 = x and 10(9y - 10) = 9x
 9y - x = 5 and 90y - 9x = 100.
9y - x = 5 and 90y - 9x = 100.
On solving, we get: x = 50.
 Length of the train is 50 m.
Length of the train is 50 m.
Discussion:
108 comments Page 2 of 11.
Anushree Kulkarni said:
3 years ago
Distance = length of the train.
D = S * T.
D = (4-2)*5/18*90,
Therefore D = 50.
D = S * T.
D = (4-2)*5/18*90,
Therefore D = 50.
(42)
Jagan Reddy said:
3 years ago
S = D/T
S-2 = D/9
9(S-2) = D ------> (1)
S-4 = D/10
10(S-4) = D ------> (2)
Distances are equal as the same cross both, equating 1,2.
10S - 40 = 9S - 18.
1S = 22(Speed of train).
Taking any one person's reference;
22-2 = D/9.
20 * 9 = D,
D = 180 * 5/18,
D = 50mtrs.
S-2 = D/9
9(S-2) = D ------> (1)
S-4 = D/10
10(S-4) = D ------> (2)
Distances are equal as the same cross both, equating 1,2.
10S - 40 = 9S - 18.
1S = 22(Speed of train).
Taking any one person's reference;
22-2 = D/9.
20 * 9 = D,
D = 180 * 5/18,
D = 50mtrs.
(18)
Talha said:
3 years ago
Hello everyone. Please have a look at my method of solution. It is giving a different answer.
Let,
the Speed of the train = x.
Then,
With respect to the first person;
The relative speed of the train = (x-2)*5/18 m/s.
Time is taken to cross the first person = 9s,
Length of the train = Speed * Time = (x-2)*(5/18)*9.
With respect to the second person;
The relative speed of the train = (x-4)*5/18 m/s.
Time is taken to cross the first person = 10s.
Length of the train = Speed * Time = (x-4)*(5/18)*10.
As both lengths are of the same body (train), so;
(x-2)*(5/18)*9 = (x-4)*(5/18)*10.
(x-2)*(5/2) = (x-4)*(25/9).
Upon solving, we get:
x = 22m.
Let,
the Speed of the train = x.
Then,
With respect to the first person;
The relative speed of the train = (x-2)*5/18 m/s.
Time is taken to cross the first person = 9s,
Length of the train = Speed * Time = (x-2)*(5/18)*9.
With respect to the second person;
The relative speed of the train = (x-4)*5/18 m/s.
Time is taken to cross the first person = 10s.
Length of the train = Speed * Time = (x-4)*(5/18)*10.
As both lengths are of the same body (train), so;
(x-2)*(5/18)*9 = (x-4)*(5/18)*10.
(x-2)*(5/2) = (x-4)*(25/9).
Upon solving, we get:
x = 22m.
(9)
Arsalan said:
4 years ago
Why we have not converted the speed of the train in m/s initially? Anyone explain it, please.
(1)
Tej said:
4 years ago
5/9 * 10 * 9 = 50.
(6)
Anand K said:
5 years ago
Treat both people separately.
1st compare person A(2 kmph) and train.
Speed = dist/time.
hence time = dist/speed.
Time(for A) = 9s.
Dist = length of train
Speed = relative speed btw A and train=(S-5/9)
S = speed of the train.
9 = LOT/(S-5/9) //LOT=Length of train.
Apply same for person B.
10=LOT/(S-10/9).
solve both equations and get;
LOT= 50mtrs.
1st compare person A(2 kmph) and train.
Speed = dist/time.
hence time = dist/speed.
Time(for A) = 9s.
Dist = length of train
Speed = relative speed btw A and train=(S-5/9)
S = speed of the train.
9 = LOT/(S-5/9) //LOT=Length of train.
Apply same for person B.
10=LOT/(S-10/9).
solve both equations and get;
LOT= 50mtrs.
Priyanshu said:
5 years ago
I didn't understand the solution, anyone explain it please.
(2)
Jayasree said:
5 years ago
Let me explain if anyone wants to know how to solve the value of x,
So we got both the equations ( 1,2 ) by solving (x/ y-5/9) = 9 and (x/ y-10/9) = 10,
9y - 5 = x ->(1) , 10(9y - 10) = 9x ->(2)
By substituting equation no (1) in equation no (2), we will get,
10(9y - 10) = 9(9y - 5),
90y - 100 = 81y - 45.
9y = 55.
| y = 55/9.
Now substitute the value of (y) in equation no (1) to get the value of (x)
9(55/9) - 5 = x.
55-5 = x.
x = 50.
Thank you.
So we got both the equations ( 1,2 ) by solving (x/ y-5/9) = 9 and (x/ y-10/9) = 10,
9y - 5 = x ->(1) , 10(9y - 10) = 9x ->(2)
By substituting equation no (1) in equation no (2), we will get,
10(9y - 10) = 9(9y - 5),
90y - 100 = 81y - 45.
9y = 55.
| y = 55/9.
Now substitute the value of (y) in equation no (1) to get the value of (x)
9(55/9) - 5 = x.
55-5 = x.
x = 50.
Thank you.
(9)
Partha said:
5 years ago
90y - 5 = x, 90y - 9x = 100.
Putting the value of x in 2nd so 90y - 81y + 45 = 100,
So after solving, y=55/9,
The put the value in any equation then we get x=50m,
Thank you.
Putting the value of x in 2nd so 90y - 81y + 45 = 100,
So after solving, y=55/9,
The put the value in any equation then we get x=50m,
Thank you.
(2)
Amigo said:
5 years ago
Instead of taking 2 variables.
Step1 : Simply find the velocity of the train. If velocity is known we can find the distance, since time is already;
Given.
(x - 5/9)*9 = (x - 10/9)*10,
81x - 45 = 90x - 100,
==> x = 55/9.
Step2 : Since we know the time for each man, take anyone say the man with velocity 10/9.
Relative velocity = (55 -10)/9 = 5/9.
Step3 : Distance = relative vel * time.
x = 5*10/9 = 50m.
Thank you.
Step1 : Simply find the velocity of the train. If velocity is known we can find the distance, since time is already;
Given.
(x - 5/9)*9 = (x - 10/9)*10,
81x - 45 = 90x - 100,
==> x = 55/9.
Step2 : Since we know the time for each man, take anyone say the man with velocity 10/9.
Relative velocity = (55 -10)/9 = 5/9.
Step3 : Distance = relative vel * time.
x = 5*10/9 = 50m.
Thank you.
(1)
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers