Aptitude - Height and Distance - Discussion
Discussion Forum : Height and Distance - General Questions (Q.No. 1)
1.
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
Answer: Option
Explanation:
Let AB be the lighthouse and C and D be the positions of the ships.
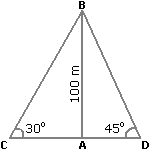
Then, AB = 100 m,  ACB = 30° and
ACB = 30° and  ADB = 45°.
ADB = 45°.
| AB | = tan 30° = | 1 |  AC = AB x 3 = 1003 m. AC = AB x 3 = 1003 m. |
| AC | 3 |
| AB | = tan 45° = 1  AD = AB = 100 m. AD = AB = 100 m. |
| AD |
 CD = (AC + AD) CD = (AC + AD) |
= (1003 + 100) m |
| = 100(3 + 1) | |
| = (100 x 2.73) m | |
| = 273 m. |
Discussion:
104 comments Page 1 of 11.
Kowsalyadevi said:
7 years ago
First, understand the problem from the given Diagram.
We have to find the distance of the CD.
So, first identify how to use 45° and 35°.
Only by using tan because we know AB value
We know that tanx = perpendicular/base.
tan 30° = AB/CA.
1/√3= 100/CA.
CA=100 x √3.
tan 45° = AB/AD.
1 = 100/AD,
AD = 100.
We know that CD = CA+CD.
= 100x√ 3+100,
= 100(√3+1),
= 100(1.73+1),
= 100(2.73),
= 273m.
We have to find the distance of the CD.
So, first identify how to use 45° and 35°.
Only by using tan because we know AB value
We know that tanx = perpendicular/base.
tan 30° = AB/CA.
1/√3= 100/CA.
CA=100 x √3.
tan 45° = AB/AD.
1 = 100/AD,
AD = 100.
We know that CD = CA+CD.
= 100x√ 3+100,
= 100(√3+1),
= 100(1.73+1),
= 100(2.73),
= 273m.
M.V.KRISHNA said:
1 decade ago
From the figure shown above
sin30=(BA/BC); sin45=(BA/BD)
=> (1/2)=(100/BC); =>(0.7071)=(100/BD)
=>BC=200m; =>BD=141.42
by pythagorean theorem:
in a rt. angled triangle, the sum of squares of the two sides
(smaller sides) of a triangle is equal to the square of third
side(larger side).
in triangle BCA
(BC)^2 = (BA)^2 +(AC)^2
(200)^2=(100)^2+(AC)^2
=>AC=173.2m
in triangle BDA
(BD)^2 = (BA)^2 +(AD)^2
(141.42)^2=(100)^2+(AC)^2
=>AC=100m
Distance between two boats=AC+AD
=>173m+100m = 273m
sin30=(BA/BC); sin45=(BA/BD)
=> (1/2)=(100/BC); =>(0.7071)=(100/BD)
=>BC=200m; =>BD=141.42
by pythagorean theorem:
in a rt. angled triangle, the sum of squares of the two sides
(smaller sides) of a triangle is equal to the square of third
side(larger side).
in triangle BCA
(BC)^2 = (BA)^2 +(AC)^2
(200)^2=(100)^2+(AC)^2
=>AC=173.2m
in triangle BDA
(BD)^2 = (BA)^2 +(AD)^2
(141.42)^2=(100)^2+(AC)^2
=>AC=100m
Distance between two boats=AC+AD
=>173m+100m = 273m
Ganesh said:
1 decade ago
Just try to understand.
We need to find AC and we know only AB.
BY P. Theorem, perpendicular/base, i.e.. AB/AC i.e., = tan.
1) We didn't know the value CB, if we take AB/CB no AC omit this.
2) AC/CB both value not known so no chance.
3) There is nothing called AC/AB mean base/perpendicular cancel this.
That's it try to read formula section you will understand.
We need to find AC and we know only AB.
BY P. Theorem, perpendicular/base, i.e.. AB/AC i.e., = tan.
1) We didn't know the value CB, if we take AB/CB no AC omit this.
2) AC/CB both value not known so no chance.
3) There is nothing called AC/AB mean base/perpendicular cancel this.
That's it try to read formula section you will understand.
Khaleeq ur rehman said:
5 years ago
According to My observation, when the angle of elevation is 45 degree then base and perpendicular must be equal which is 100 according to AD measurement if another elevation is less then from another which is 30 degree of AC then how is possible that distance/length of AC increase from another distance. Please anyone explain.
(5)
Prasad said:
6 years ago
@All.
Know, how we get the 'tan'.
In the question is given we have to find the distance then that time we are not treating the angle of elevation so we have to take distance and hight then the formula becomes;
Tan=opp/adj.
Then AB/AC look at the figure it will be clear for you.
Know, how we get the 'tan'.
In the question is given we have to find the distance then that time we are not treating the angle of elevation so we have to take distance and hight then the formula becomes;
Tan=opp/adj.
Then AB/AC look at the figure it will be clear for you.
(1)
Bhanu said:
1 decade ago
Section A of 5th standard has a class strength of 40 with an average height of 100.5 cm. Section B has a class.
Strength of 50 with an average height of 96 cm. What is the weighted average height of students in the 5th.
Standard? (Rounded to the nearest 0.5 cm).
Strength of 50 with an average height of 96 cm. What is the weighted average height of students in the 5th.
Standard? (Rounded to the nearest 0.5 cm).
AKASH RAI said:
9 years ago
Then, AB = 100 m, ACB = 30° and ADB = 45°.
AB = tan 30° = 1, AC = AB x 3 = 1003 m.
AC = 1003 m.
AB = tan 45° = 1, AD = AB = 100 m.
AD
CD = (AC + AD) = (1003 + 100) m.
= 100(3 + 1).
= (100 x 2.73) m.
= 273 m.
That Proved.
AB = tan 30° = 1, AC = AB x 3 = 1003 m.
AC = 1003 m.
AB = tan 45° = 1, AD = AB = 100 m.
AD
CD = (AC + AD) = (1003 + 100) m.
= 100(3 + 1).
= (100 x 2.73) m.
= 273 m.
That Proved.
Akshay said:
3 years ago
Short tricks
(1)30_60_90
1:√3:2.
So,
∆adb
a = 1×100.
= 100m.
b = √3×100.
= 173m.
d = 100 × 2
= 200m.
(2) 45_45_90
1:1:√2.
∆dcb
C = 1×100.
= 100m.
B = 1×100,
= 100m.
D = √2×100.
= 141m.
Total
ADC = 173 + 100,
= 273m.
(1)30_60_90
1:√3:2.
So,
∆adb
a = 1×100.
= 100m.
b = √3×100.
= 173m.
d = 100 × 2
= 200m.
(2) 45_45_90
1:1:√2.
∆dcb
C = 1×100.
= 100m.
B = 1×100,
= 100m.
D = √2×100.
= 141m.
Total
ADC = 173 + 100,
= 273m.
(12)
Bhavarth said:
5 years ago
@Kanishka Roy.
The one which is opposite to angle will be height.
And one which is adjacent to angle will be base.
Note that the one which is the base is not the longest side of triangle otherwise it would be the hypotenuse.
The one which is opposite to angle will be height.
And one which is adjacent to angle will be base.
Note that the one which is the base is not the longest side of triangle otherwise it would be the hypotenuse.
Srinureddy said:
1 decade ago
Hello friends. As best of my knowledge. Here we find the distance between two ships i.e. (AC+AD).
Here we know the height of the lighthouse (AB=100m). For the sake of we taken only (TAN = AB/AC). But not take. Sin&Cos.
Here we know the height of the lighthouse (AB=100m). For the sake of we taken only (TAN = AB/AC). But not take. Sin&Cos.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers