Aptitude - Height and Distance - Discussion
Discussion Forum : Height and Distance - General Questions (Q.No. 1)
1.
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
Answer: Option
Explanation:
Let AB be the lighthouse and C and D be the positions of the ships.
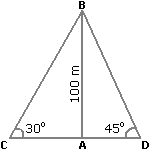
Then, AB = 100 m, 
ACB = 30° and ADB = 45°.
| AB | = tan 30° = | 1 |  AC = AB x 3 = 1003 m. |
| AC | 3 |
| AB | = tan 45° = 1 AD = AB = 100 m. |
| AD |
 CD = (AC + AD) |
= (1003 + 100) m |
| = 100(3 + 1) | |
| = (100 x 2.73) m | |
| = 273 m. |
Discussion:
104 comments Page 1 of 11.
Sunitha said:
1 decade ago
How to find out root 3?
(1)
Ravi said:
1 decade ago
Why we take AB/AC, AB/AD?
Sam said:
1 decade ago
Just remember root3=1.73 and root2=1.41
we take ab/ac because we want to find ac and we only know ab thats it
we take ab/ac because we want to find ac and we only know ab thats it
Srikanth said:
1 decade ago
Why you taken Tan and why you not taken cos ?
Jowy said:
1 decade ago
The tan30 is root(3) divide by 3. So how did you get root(3) ?
Mouli said:
1 decade ago
I am not understand jowy said.
M.V.KRISHNA said:
1 decade ago
From the figure shown above
sin30=(BA/BC); sin45=(BA/BD)
=> (1/2)=(100/BC); =>(0.7071)=(100/BD)
=>BC=200m; =>BD=141.42
by pythagorean theorem:
in a rt. angled triangle, the sum of squares of the two sides
(smaller sides) of a triangle is equal to the square of third
side(larger side).
in triangle BCA
(BC)^2 = (BA)^2 +(AC)^2
(200)^2=(100)^2+(AC)^2
=>AC=173.2m
in triangle BDA
(BD)^2 = (BA)^2 +(AD)^2
(141.42)^2=(100)^2+(AC)^2
=>AC=100m
Distance between two boats=AC+AD
=>173m+100m = 273m
sin30=(BA/BC); sin45=(BA/BD)
=> (1/2)=(100/BC); =>(0.7071)=(100/BD)
=>BC=200m; =>BD=141.42
by pythagorean theorem:
in a rt. angled triangle, the sum of squares of the two sides
(smaller sides) of a triangle is equal to the square of third
side(larger side).
in triangle BCA
(BC)^2 = (BA)^2 +(AC)^2
(200)^2=(100)^2+(AC)^2
=>AC=173.2m
in triangle BDA
(BD)^2 = (BA)^2 +(AD)^2
(141.42)^2=(100)^2+(AC)^2
=>AC=100m
Distance between two boats=AC+AD
=>173m+100m = 273m
Krishna said:
1 decade ago
Why we used Tan please clarify ?
Periyasamy said:
1 decade ago
Can you please give us notes of trignometric formulas which are used to solve height and length problems?
Ankit said:
1 decade ago
Why you taken Tan and why you not taken cos ?
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers