IndiaBIX

Aptitude - Height and Distance

Exercise : Height and Distance - General Questions
1.
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
173 m
200 m
273 m
300 m
Answer: Option
Explanation:

Let AB be the lighthouse and C and D be the positions of the ships.

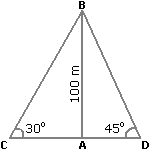
Then, AB = 100 m, ACB = 30° and ADB = 45°.

AB = tan 30° = 1         AC = AB x 3 = 1003 m.
AC 3

AB = tan 45° = 1         AD = AB = 100 m.
AD

CD = (AC + AD) = (1003 + 100) m
= 100(3 + 1)
= (100 x 2.73) m
= 273 m.

2.
A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30° with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60°. What is the distance between the base of the tower and the point P?
43 units
8 units
12 units
Data inadequate
None of these
Answer: Option
Explanation:

One of AB, AD and CD must have given.

So, the data is inadequate.

3.
The angle of elevation of a ladder leaning against a wall is 60° and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:
2.3 m
4.6 m
7.8 m
9.2 m
Answer: Option
Explanation:

Let AB be the wall and BC be the ladder.

Then, ACB = 60° and AC = 4.6 m.

AC = cos 60° = 1
BC 2

BC = 2 x AC
= (2 x 4.6) m
= 9.2 m.

4.
An observer 1.6 m tall is 203 away from a tower. The angle of elevation from his eye to the top of the tower is 30°. The height of the tower is:
21.6 m
23.2 m
24.72 m
None of these
Answer: Option
Explanation:

Let AB be the observer and CD be the tower.

Draw BE CD.

Then, CE = AB = 1.6 m,

      BE = AC = 203 m.

DE = tan 30° = 1
BE 3

DE = 203 m = 20 m.
3

CD = CE + DE = (1.6 + 20) m = 21.6 m.

5.
From a point P on a level ground, the angle of elevation of the top tower is 30°. If the tower is 100 m high, the distance of point P from the foot of the tower is:
149 m
156 m
173 m
200 m
Answer: Option
Explanation:

Let AB be the tower.

Then, APB = 30° and AB = 100 m.

AB = tan 30° = 1
AP 3

AP = (AB x 3) m
= 1003 m
= (100 x 1.73) m
= 173 m.

Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers