IndiaBIX

Verbal Reasoning - Arithmetic Reasoning

Exercise : Arithmetic Reasoning - Section 2
26.
Nitin's age was equal to square of some number last year and the following year it would be cube of a number. If again Nitin's age has to be equal to the cube of some number, then for how long he will have to wait?
10 years
38 years
39 years
64 years
Answer: Option
Explanation:

Clearly, we have to first find two numbers whose difference is 2 and of which the smaller one is a perfect square and the bigger one a perfect cube.

Such numbers are 25 and 27.

Thus, Nitin is now 26 years old. Since the next perfect cube after 27 is 64,

so required time period = (64 - 26) years = 38 years.

27.
On Children's Day, sweets were to be equally distributed among 175 children in a school. Actually on the Children's Day, 35 children were absent and therefore each child got 4 sweets extra. Total how many sweets were available for distribution ?
2400
2480
2680
2800
Answer: Option
Explanation:

28.
Between two book-ends in your study are displayed your five favourite puzzle books. If you decide to arrange the five books in every possible combination and moved just one book every minute, how long would it take you ?
1 hour
2 hours
3 hours
4 hours
Answer: Option
Explanation:

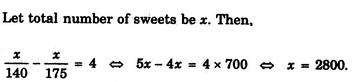
Clearly, number of ways of arranging 5 books = 5 ! = 5 x 4 x 3 x 2 x 1 = 120.

So, total time taken = 120 minutes = 2 hours.

29.
A placed three sheets with two carbons to get two extra copies of the original. Then he decided to get more carbon copies and folded the paper in such a way that the upper half of the sheets were on top of the lower half. Then he typed. How many carbon copies did he get?
1
2
3
4
Answer: Option
Explanation:

Since the number of carbons is 2, only two copies can be obtained.

30.
A printer numbers the pages of a book starting with 1 and uses 3189 digits in all. How many pages does the book have ?
1000
1074
1075
1080
Answer: Option
Explanation:

No. of digits in 1-digit page nos. = 1x9 = 9.

No. of digits in 2-digit page nos. = 2 x 90 = 180.

No. of digits in 3-digit page nos. = 3 x 900 = 2700.

No. of digits in 4-digit page nos. = 3189 - (9 + 180 + 2700) = 3189 - 2889 = 300.

Therefore No. of pages with 4-digit page nos. = (300/4) = 75.

Hence, total number of pages = (999 + 75) = 1074.

Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers