Online Engineering Mechanics Test - Engineering Mechanics Test 9
- This is a FREE online test. Beware of scammers who ask for money to attend this test.
- Total number of questions: 20.
- Time allotted: 30 minutes.
- Each question carries 1 mark; there are no negative marks.
- DO NOT refresh the page.
- All the best!
Marks : 2/20
Test Review : View answers and explanation for this test.
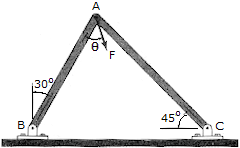
Determine the magnitude and direction  of F so that this force has components of 40 lb acting from A toward B and 60lb acting from A toward C on the frame.
of F so that this force has components of 40 lb acting from A toward B and 60lb acting from A toward C on the frame.
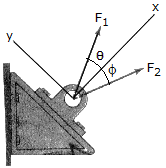
If F1 = F2 = 30lb, determine the angles  and
and  so that the resultant force is directed along the positive x axis and has a magnitude of FR = 20 lb.
so that the resultant force is directed along the positive x axis and has a magnitude of FR = 20 lb.
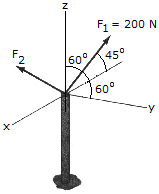
Determine the magnitude and direction angles of F2, so that the resultant of the two forces acts upward along the z axis of the pole and has a magnitude of 275 N.

Cable BC exerts a force of F = 28 N on the top of the flagpole. Determine the projection of this force along the positive z axis of the pole.

Determine the moment of the force at A about point P. Use a vector analysis and express the result in Cartesian vector form.

Determine the magnitude and direction of the couple shown.
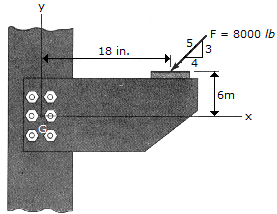
This structural connection is subjected to the 8,000-lb force. Replace this force by an equivalent force and couple acting at the center of the bolt group, O.

Replace the loading system acting on the post by an equivalent force and couple system at point O.

The wind has blown sand over a platform such that the intensity of load can be approximated by the function  . Simplify this distributed loading to a single concentrated force and specify the magnitude and location of the force measured from A.
. Simplify this distributed loading to a single concentrated force and specify the magnitude and location of the force measured from A.

The girl has a mass of 17kg and mass center at Gg, and the tricycle has a mass of 10kg and mass center at Gt. Determine the normal reactions at each wheel for equilibrium.

The hoist supports the 125-kg engine. Determine the force the load creates in member DB and in member FB, which contains the hydraulic cylinder H.
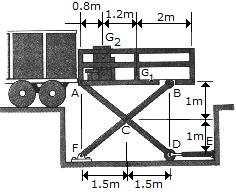
The scissors lift consists of two sets of symmetrically placed cross members (one in front that is shown and one behind that is not shown) and two hydraulic cylinders (front [labeled DE] and back [not shown]). The uniform platform has a mass of 60 kg with a center of gravity at G1. The 85 kg load (center of gravity at G2) is centered front to back. Determine the force in each of the hydraulic cylinders necessary to maintain equilibrium. These are rollers at B and D.
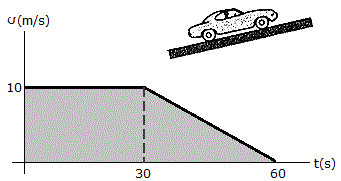
A car travels up a hill with the speed shown in the graph. Compute the total distance the car moves until it stops at t = 60 s. What is the acceleration at t = 45 s?
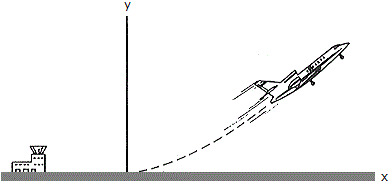
The flight path of a jet aircraft as it takes off is defined by the parmetric equations x = 1.25 t2 and y = 0.03 t3, where t is the time after take-off, measured in seconds, and x and y are given in meters. At t = 40 s (just before it starts to level off), determine at this instant (a) the horizontal distance it is from the airport, (b) its altitude, (c) its speed and (d) the magnitude of its acceleration.
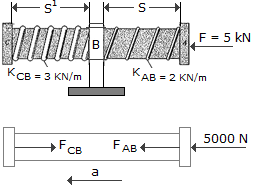
The 2-kg shaft CA passes through a smooth journal bearing at B. Initially, the springs, which are coiled loosely around the shaft, are unstretched when no force is applied to the shaft. In this position s = sª = 250 and the shaft is originally at rest. If a horizontal force of F = 5 kN is applied, determine the speed of the shaft at the instant s = 50 mm, sª = 450 mm. The ends of the springs are attached to the bearing at B and the caps at C and A.
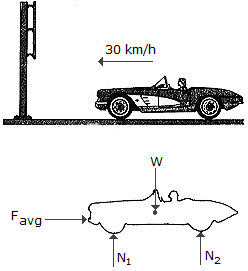
A car having a mass of 2 Mg strikes a smooth, rigid sign post with an initial speed of 30 km/h. To stop the car, the front end horizontally deforms 0.2 m. If the car is free to roll during the collision, determine the average horizontal collision force causing the deformation.
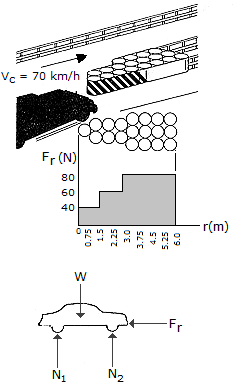
A car, assumed to be rigid and having a mass of 800 kg, strikes a barrel-barrier installation without the driver applying the brakes. From experiments, the magnitude of the force of resistance Fr, created by deforming the barrels successively, is shown as a function of vehicle penetration. If the car strikes the barrier traveling at Vc = 70 km/h, determine approximately the distance s to which the car penetrates the barrier.
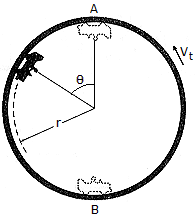
The "flying car" is a ride at an amusement park, which consists of a car having wheels that roll along a track mounted on a drum. Motion of the car is created by applying the car's brake, thereby gripping the car to the track and allowing it to move with a speed of vt = 3m/s. If the rider applies the brake when going from B to A and then releases it at the top of the drum, A, so that the car coasts freely down along the track to B ( =
= 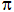 rad), determine the speed of the car at B and the normal reaction which the drum exerts on the car at B. The rider and car have a total mass of m = 250 kg and the center of mass of the car and rider moves along a circular path of radius r = 8 m.
rad), determine the speed of the car at B and the normal reaction which the drum exerts on the car at B. The rider and car have a total mass of m = 250 kg and the center of mass of the car and rider moves along a circular path of radius r = 8 m.
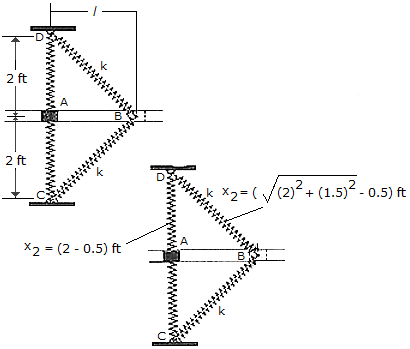
The book A having a weight of 1.5 lb slides on the smooth horizontal slot. If the block is drawn back so that s = 0. Each of the two springs has a stiffness of k = 150 lb/ft and an unstretched length of 0.5 ft.
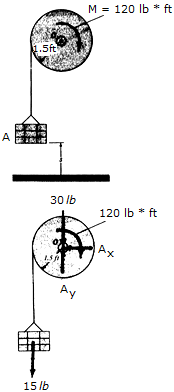
A motor supplies a constant torque or twist of M = 120 lb • ft to the drum. If the drum has a weight of 30 lb and a radius of gyration of k0 = 0.8ft, determine the speed of the 15-lb carte A after it rises s = 4 ft starting from rest. Neglect the weight of the cord.
 = 54.9°,
= 54.9°,  = 114.0°,
= 114.0°, 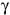 = 44.7°
= 44.7°