Non Verbal Reasoning - Analytical Reasoning - Discussion
What is the minimum number of different colours required to paint he given figure such that no two adjacent regions have the same colour?
The figure may be labelled as shown.
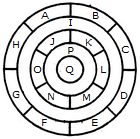
The regions A, C, E and G can have the same colour say colour 1.
The regions B, D, F and H can have the same colour (but different from colour 1) say colour 2.
The region 1 lies adjacent to each one of the regions A, B, C, D, E, F, G and H and therefore it should have a different colour say colour 3.
The regions J, L and N can have the same colour (different from colour 3) say colour 1.
The regions K, M and O can have the same colour (different fromthe colours 1 and 3). Thus, these regions will have colour 2.
The region P cannot have any of the colours 1 and 2 as it lies adjacent to each one of the regions J, K, L, M, N and O and so it will have colour 3.
The region Q can have any of the colours 1 or 2.
Minimum number of colours required is 3.
Up to Q is 17=>17/2=8.
Why you divided by 2?
A is 1, B is 2,C is 3. Upto Q is 17 =>17/2=8 and remainder 1.
Add divisor + remainder.
So minimum Colorol is 3.