Non Verbal Reasoning - Analytical Reasoning
- Analytical Reasoning - Section 1
- Analytical Reasoning - Section 2
Count the number of triangles and squares in the given figure.
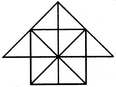
The figure may be labelled as shown.
Triangles:
The simplest triangles are JBO, BKO, KDO, DFO, FGO, GHO, HIO, IJO, ABJ, BCK, CKD and DEF i.e.12 in number.
The triangles composed of two components each are IBO, BDO, DGO, GIO, ABO, CDO, CBO, CBD and DEO i.e. 9 in number.
The triangles composed of four components each are IBD, BDG, DGI, GIB, ACO and COE i.e. 6 in number.
There is only one. triangle i.e. ACE composed of eight components.
Thus, there are 12 + 9 + 6 + 1 = 28 triangles in the given figure.
Squares:
The squares composed of two components each are BKOJ, KDFO, OFGH and JOHI i.e. 4 in number.
There is only one square i.e. CDOB composed of four components.
There is only one square i.e. BDGI composed of eight components.
Thus, there are 4 + 1 + 1 = 6 squares in the given figure.
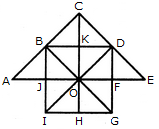
What is the minimum number of different colours required to paint he given figure such that no two adjacent regions have the same colour?
The figure may be labelled as shown.
The regions A, C, E and G can have the same colour say colour 1.
The regions B, D, F and H can have the same colour (but different from colour 1) say colour 2.
The region 1 lies adjacent to each one of the regions A, B, C, D, E, F, G and H and therefore it should have a different colour say colour 3.
The regions J, L and N can have the same colour (different from colour 3) say colour 1.
The regions K, M and O can have the same colour (different fromthe colours 1 and 3). Thus, these regions will have colour 2.
The region P cannot have any of the colours 1 and 2 as it lies adjacent to each one of the regions J, K, L, M, N and O and so it will have colour 3.
The region Q can have any of the colours 1 or 2.
Minimum number of colours required is 3.
Count the number of triangles and squares in the given figure.
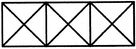
The figure may be labelled as shown.
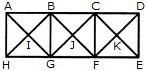
Triangles :
The, simplest triangles are ABI, BGI, GHI, HAI, BCJ, CFJ, FGJ, GBJ, CDK, DEK, EFK and FCK i.e. 12 in number.
The triangles composed of two components each are ABG, BGH, GHA, HAB, BCF, CFG, FGB, GBC, CDE, DEF, EFC and FGD i.e. 12 in number.
The triangles composed of four components each are AGC, BFD, HBF and GCE i.e.4 in number.
Thus, there are 12 + 12 + 4 = 28 triangles in the given figure.
Squares :
The squares composed of two components each are BJGI and CKFJ i.e. 2 in number.
The squares composed of four components each are ABGH, BCFG and CDEF i.e. 3 in number.
Total number of squares in the figure = 2 + 3 = 5.
Count the number of parallelogram in the given figure.
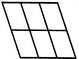
The figure may be labelled as shown.
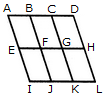
The simplest ||gms are ABFE, BCGF, CDHG, EFJI, FGKJ and GHLK. These are 6 in number.
The parallelograms composed of two components each are ACGE, BDHF, EGKI, FHLJ, ABJI, BCKJ and CDLK. Thus, there are 7 such parallelograms.
The parallelograms composed of three components each are ADHE and EHLI i.e. 2 in number.
The parallelograms composed of four components each are ACKI and BDLJ i.e. 2 in number
There is only one parallelogram composed of six components, namely ADLI.
Thus, there are 6 + 7 + 2 + 2 + 1 = 18 parallelograms in the figure.
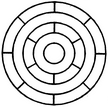
In the adjoining figure, if the centres of all the circles are joined by horizontal and vertical lines, then find the number of squares that can be formed.
The figure may be labelled as shown.
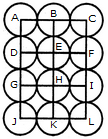
We shall join the centres of all the circles by horizontal and vertical lines and then label the resulting figure as shown.
The simplest squares are ABED, BCFE, DEHG, EFIH, GHKJ and HILK i.e. 6 in number.
The squares composed of four simple squares are ACIG and DFLJ i.e. 2 in number.
Thus, 6 + 2 = 8 squares will be formed.