Non Verbal Reasoning - Analytical Reasoning

The figure may be labelled as shown.

The simplest squares are ABGF, BCHG, CDIH, DEJI, FGLK, GHML, HINM, IJON, KLQP, LMRQ, MNSR, NOTS, PQVU, QRWV, RSXW and STYX i.e. 16 in number.

The squares composed of four components each are ACMK, BDNL, CEOM, FHRP, GISQ, HJTR, KMWU, LNXV and MOYW i.e. 9 in number.

The squares composed of nine components each are ADSP, BETQ, FIXU and GJYV i.e. 4 in number.

There is one square AEYU composed of sixteen components.

There are 16 + 9 + 4 + 1 = 30 squares in the given figure.

The figure may be labelled as shown.

The quadrilaterals in the figure are ABCD, ABDE, ABDF, ABDH, CDHA, CDEA, CDFA, DEAG, DEFA, FAGD and AGDH.

The number of quadrilaterals in the figure is 11.

The figure may be labelled as shown.

The simplest squares are QUYX, URVY, YVSW and XYWT i.e. 4 in number.

The squares composed of two components each are IMYP, MJNY, YNKO and PYOL i.e. 4 in number.

The squares composed of three components each are AEYH, EBFY, YFCG and HYGD i.e. 4 in number.

There is only one square i.e. QRST composed of four components.

There is only one square i.e. IJKL composed of eight components.

There is only one square i.e. ABCD composed of twelve components.

Total number of squares in the given figure = 4 + 4 + 4+1 + 1 + 1 = 15.

The figure may be labelled as shown.

The spaces P, Q and R have to be shaded by three different colours definitely (since each of these three spaces lies adjacent to the other two).

Now, in order that no two adjacent spaces be shaded by the same colour, the spaces T, U and S must be shaded with the colours of the spaces P, Q and R respectively.

Also the spaces X, V and W must be shaded with the colours of the spaces S, T and U respectively i.e. with the colours of the spaces R, P and Q respectively. Thus, minimum three colours are required.

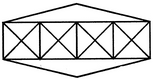
The figure may be labelled as shown.

Triangles:

The simplest triangles are BGM, GHM, HAM, ABM, GIN, UN, JHN, HGN, IKO, KLO, LJO, JIO, KDP, DEP, ELP, LKP, BCD and AFE i.e. 18 in number.

The triangles composed of two components each are ABG, BGH, GHA, HAB, HGI, GIJ, IJH, JHG, JIK, IKL, KLJ, LJI, LKD, KDE, DEL and ELK i.e. 16 in number.

The triangles composed of four components each are BHI, GJK, ILD, AGJ, HIL and JKE i.e. 6 in number.

Total number of triangles in the figure = 18 +16 + 6 = 40.

Squares :

The squares composed of two components each are MGNH, NIOJ and OKPL i.e. 3 in number.

The squares composed of four components each are BGHA, GIJH, IKLJ and KDEL i.e. 4 in number.

Total number of squares in the figure = 3 + 4 = 7.