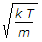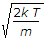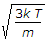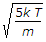Mechanical Engineering - Thermodynamics - Discussion
Discussion Forum : Thermodynamics - Section 1 (Q.No. 16)
16.
The most probable velocity of the gas molecules is given by
Discussion:
33 comments Page 1 of 4.
HIREN said:
10 years ago
The most probable speed, vp, is the speed most likely to be possessed by any molecule (of the same mass m) in the system and corresponds to the maximum value or mode of f(v). To find it, we calculate df/dv, set it to zero and solve for v:
\frac{df(v)}{dv} = 0
which yields:
v_p = \sqrt {\frac{2kT}{m}} = \sqrt {\frac{2RT}{M}}
The root mean square speed is the second-order moment of speed:
= \sqrt {\langle v^2 \rangle} = \left(\int_0^{\infty} v^2 \, f(v) \, dv \right)^{1/2}.
= \sqrt {\frac{3kT}{m}} = \sqrt {\frac{3RT}{M} } = \sqrt{\frac{3}{2}} v_p.
\frac{df(v)}{dv} = 0
which yields:
v_p = \sqrt {\frac{2kT}{m}} = \sqrt {\frac{2RT}{M}}
The root mean square speed is the second-order moment of speed:
= \sqrt {\langle v^2 \rangle} = \left(\int_0^{\infty} v^2 \, f(v) \, dv \right)^{1/2}.
= \sqrt {\frac{3kT}{m}} = \sqrt {\frac{3RT}{M} } = \sqrt{\frac{3}{2}} v_p.
Rathi said:
1 decade ago
The most probable speed, vp, is the speed most likely to be possessed by any molecule (of the same mass m) in the system and corresponds to the maximum value or mode of f(v). To find it, we calculate df/dv, set it to zero and solve for v:
\frac{df(v)}{dv} = 0
which yields:
v_p = \sqrt { \frac{2kT}{m} } = \sqrt { \frac{2RT}{M} }
Ref : http://en.wikipedia.org/wiki/Maxwell%E2%80%93Boltzmann_distribution#Distribution_for_relative_speed
\frac{df(v)}{dv} = 0
which yields:
v_p = \sqrt { \frac{2kT}{m} } = \sqrt { \frac{2RT}{M} }
Ref : http://en.wikipedia.org/wiki/Maxwell%E2%80%93Boltzmann_distribution#Distribution_for_relative_speed
Biplab said:
9 years ago
μ rms = √ (3RT/M).
where
μrms = root mean square velocity in m/sec.
R = ideal gas constant = 8.3145 (kg.m2/sec2)/Kmol.
T = absolute temperature in Kelvin.
M = mass of a mole of the gas in kilograms.
where
μrms = root mean square velocity in m/sec.
R = ideal gas constant = 8.3145 (kg.m2/sec2)/Kmol.
T = absolute temperature in Kelvin.
M = mass of a mole of the gas in kilograms.
Krishna said:
1 decade ago
While here many got doubts about B & C options. I goggled it and found that the word 'Probable velocity makes the difference here.
Option : B is correct.
Option C is RMS velocity of molecules.
Option : B is correct.
Option C is RMS velocity of molecules.
Rajesh rank said:
8 years ago
Answer B. Probable velocity of the gas molecules.
Answer C. Typical velocity of molecules in a gas.
In the question, they asked probable velocity so Answer B is right.
Answer C. Typical velocity of molecules in a gas.
In the question, they asked probable velocity so Answer B is right.
Engr. Amir Shehzad said:
3 years ago
K.E is directly proportional to Temperature.
1/2mv^2 = kT.
v^2 = 2kT/m.
So v=√(2kT/m).
Where k= proportionality constant.
1/2mv^2 = kT.
v^2 = 2kT/m.
So v=√(2kT/m).
Where k= proportionality constant.
(15)
Shubham Ganesh Rakshe said:
9 years ago
Then how to find most probable velocity?
Please mention the method just like you explained about root mean square velocity.
Please mention the method just like you explained about root mean square velocity.
Rishi said:
1 decade ago
Answer 2 is correct. The third answer (C) is for root mean square velocity. And 2nd (B) is the most probable velocity.
Vinay said:
1 decade ago
Formula for most probable velocity.
vp = option B.
And for root mean square velocity.
Vrms=option C.
vp = option B.
And for root mean square velocity.
Vrms=option C.
Prasad said:
1 decade ago
I guess it is option C. The rms velocity itself is most probable velocity. Please if any one clarify.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers