Engineering Mechanics - Kinematics of Particle (KOP) - Discussion
Discussion Forum : Kinematics of Particle (KOP) - General Questions (Q.No. 32)
32.
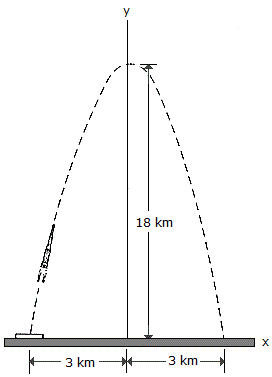
For a short time the missile moves along the parabolic path y = (18 - 2x2) km. If motion along the ground is measured as x = (4t - 3) km, where t is in seconds, determine the magnitudes of the missile's velocity and acceleration when t = 1 s.
Discussion:
1 comments Page 1 of 1.
Hermes said:
5 years ago
y = 18 - 2x^2,
= 18 -2(4t-3)^2,
= -32t^2 + 48t.
Vy = dy/dt,
= -64t + 48.
ay = dv/dt,
= -64.
x = 4t -3.
Vx = dx/dt.
= 4,
ax = dx/dt.
= 0.
when t = 1s.
Vy = -16 km/s^2,
Vx = 4 km/s^2.
v = √(Vy^2 + Vx^2),
= 16.49 km/s^2.
ay = -64 km/s^2.
ax = 0 km/s^2,
a = √(ax^2 + ay^2),
= 64 km/s^2.
= 18 -2(4t-3)^2,
= -32t^2 + 48t.
Vy = dy/dt,
= -64t + 48.
ay = dv/dt,
= -64.
x = 4t -3.
Vx = dx/dt.
= 4,
ax = dx/dt.
= 0.
when t = 1s.
Vy = -16 km/s^2,
Vx = 4 km/s^2.
v = √(Vy^2 + Vx^2),
= 16.49 km/s^2.
ay = -64 km/s^2.
ax = 0 km/s^2,
a = √(ax^2 + ay^2),
= 64 km/s^2.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers