Electrical Engineering - Circuit Theorems and Conversions - Discussion
Discussion Forum : Circuit Theorems and Conversions - General Questions (Q.No. 3)
3.
Find the total current through R3 in the given circuit.
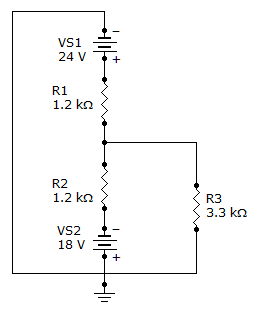

Discussion:
40 comments Page 1 of 4.
Krupa said:
6 months ago
VS1-VS2 = 6V,
I = V/R.
I = 6/3.3k.
I = 1.81mA.
I = V/R.
I = 6/3.3k.
I = 1.81mA.
(1)
Albert said:
3 years ago
Yes, @Stoyan.
0.769mA is my answer using mesh analysis.
0.769mA is my answer using mesh analysis.
(14)
Egni said:
3 years ago
Please clarify at which point the lowest point of R3 connects it to the ground.
(1)
Syed Zakeer said:
4 years ago
The answer is,
R3 = VS1-VS2*R3 = 1.8mA.
R3 = VS1-VS2*R3 = 1.8mA.
(5)
Calculuseuler said:
6 years ago
The 1.2k and the 18v source, are open leaving 24v source connected in series with the other two.
So, the current through 3.3k.
= 24/3.3,
=7.3mA.
So, the current through 3.3k.
= 24/3.3,
=7.3mA.
(5)
Anon said:
6 years ago
I don't agree with the 6V Vth since the circuit has aiding voltages.
(1)
Sivakumar.G said:
7 years ago
24-18 = 6v.
Total current through r3.
r3 = 3.3.
I = V/R.
I = 6/3.3.
I = 1.80.
Total current through r3.
r3 = 3.3.
I = V/R.
I = 6/3.3.
I = 1.80.
(5)
Sikandar said:
7 years ago
No, the Correct ans is 5.3mA. So option B is correct.
(2)
Bibek said:
8 years ago
@Mayur.
Can you help me by explaining how you have calculated Thevenin Voltage?
Can you help me by explaining how you have calculated Thevenin Voltage?
Kiruthika said:
8 years ago
I also got the answer 0.769mA.
(1)
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers