Electrical Engineering - Circuit Theorems and Conversions - Discussion
Discussion Forum : Circuit Theorems and Conversions - General Questions (Q.No. 3)
3.
Find the total current through R3 in the given circuit.
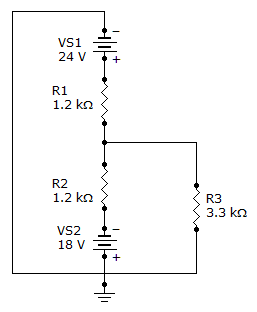

Discussion:
40 comments Page 4 of 4.
Harsh Sharma said:
1 decade ago
If you want the answer by nodal analysis,
See that the 18 we source is coming in front of 24 we source because in between their path no element is connected.
So while writing kcl we have [ 24 - 18 ] = 6 we source above the 1.2k resistor.
By that you solve and will get the answer as 1.8 mA.
Answer can also be given by source transformation technique.
Try it once also interesting to analyse the circuit.
See that the 18 we source is coming in front of 24 we source because in between their path no element is connected.
So while writing kcl we have [ 24 - 18 ] = 6 we source above the 1.2k resistor.
By that you solve and will get the answer as 1.8 mA.
Answer can also be given by source transformation technique.
Try it once also interesting to analyse the circuit.
Pocahontas said:
1 decade ago
The answer that I've got is 0.769mA using the superposition theorem.
Wee kian said:
1 decade ago
So is R2 or R3. the diagram is so misleading. does the VS1 connected to ground or just R3?
Bettycroger said:
1 decade ago
The question asked for the current through R3 = 3.3kohm
Adnan CECOSIAN said:
1 decade ago
Use mesh analysis:
Create two loops then apply KVL we get 2 equations
Loop1; (1.2k)(I1)+(1.2k)(I1+I2)=24
Loop2: (1.2k)(I2)+(1.2k)(I1+I2)=-18
Rearrange these two equations
then find Whole Deterimnent which i found
=4.32k^2
use cramer Rule
I1=18.35mA
and I2=16.6mA
now therefore current through 1.2kohm Resistor is
I1+I2=18.35-16.6
=1.75mA
So Answer D is correct.
Create two loops then apply KVL we get 2 equations
Loop1; (1.2k)(I1)+(1.2k)(I1+I2)=24
Loop2: (1.2k)(I2)+(1.2k)(I1+I2)=-18
Rearrange these two equations
then find Whole Deterimnent which i found
=4.32k^2
use cramer Rule
I1=18.35mA
and I2=16.6mA
now therefore current through 1.2kohm Resistor is
I1+I2=18.35-16.6
=1.75mA
So Answer D is correct.
REDDI said:
1 decade ago
We apply the kirchoff current law
(V-24/1.2)+(V+18/1.2)+(V/3.3)=0
we get V=2.55Mv
I=V/R=(2.55/3.3)=0.77mA
(V-24/1.2)+(V+18/1.2)+(V/3.3)=0
we get V=2.55Mv
I=V/R=(2.55/3.3)=0.77mA
Ronit said:
1 decade ago
The answer I'm getting is 0.77mA.
Can anyone explain it - How do they get the answer 1.8mA ?
Can anyone explain it - How do they get the answer 1.8mA ?
(2)
M.V.KRISHNA/PALVONCHA said:
1 decade ago
You are right Beth Tate.
Krishnan said:
1 decade ago
Can any one explain the answer more clearly?
Beth Tate said:
1 decade ago
If you do the node analysis on this problem, you get your current to be .769 mA. By splitting the above circuit into two sections with 2 diffferent currents, you also get .769 mA. How do you come to get the answer 1.8 mA ?
(1)
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers