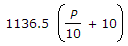IndiaBIX

Civil Engineering - Water Supply Engineering

Exercise : Water Supply Engineering - Section 3
26.
The depth of the water table at a place is 45 m below the general ground level. To lift water from a deep tube well in such a locality, the type of pump to be installed is
Centrifugal pump
Reciprocating pump
Deep well turbine pump
None of these.
Answer: Option
Explanation:
No answer description is available. Let's discuss.
27.
Critical time for developing a water hammer, is the time required for
closing the valve
the wave to travel from valve to the reservoir
the wave to travel from the valve to the reservoir and back
none of these.
Answer: Option
Explanation:
No answer description is available. Let's discuss.
28.
According to Buston's formula, fire demand in litres per minute for a population of P thousands, is
3182 P
4637 P (1 - 0.01 P)
5663 P
none of these.
Answer: Option
Explanation:
No answer description is available. Let's discuss.
29.
The ratio of maximum hourly consumption and average hourly consumption of the maximum day, is
1.2
1.5
1.8
2.4
2.7
Answer: Option
Explanation:
No answer description is available. Let's discuss.
30.
Cast iron pipes are generally preferred to, because
of moderate cost
of ease to join
of durability
of longer life
all the above.
Answer: Option
Explanation:
No answer description is available. Let's discuss.
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers