Aptitude - Problems on Trains - Discussion
Discussion Forum : Problems on Trains - General Questions (Q.No. 27)
27.
A train overtakes two persons who are walking in the same direction in which the train is going, at the rate of 2 kmph and 4 kmph and passes them completely in 9 and 10 seconds respectively. The length of the train is:
Answer: Option
Explanation:
| 2 kmph = |  |
2 x | 5 |  |
m/sec = | 5 | m/sec. |
| 18 | 9 |
| 4 kmph = | |
4 x | 5 | |
m/sec = | 10 | m/sec. |
| 18 | 9 |
Let the length of the train be x metres and its speed by y m/sec.
| Then, |  |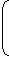
x |  |
= 9 and | |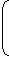
x | |
= 10. |
|
|
9y - 5 = x and 10(9y - 10) = 9x
9y - x = 5 and 90y - 9x = 100.
On solving, we get: x = 50.
Length of the train is 50 m.
Discussion:
106 comments Page 8 of 11.
Krishna said:
9 years ago
@All.
Please anyone give the answer of Durga's question, I have the same question.
Please anyone give the answer of Durga's question, I have the same question.
Sathees said:
9 years ago
Equ 1 is => x = (9y - 5) /9 * 9 = 9 y - 5 => 5 = 9y - 5.
Equ 2 is => x = (9y - 10) /9 *10.
9 x = (9y - 10) * 10.
9x = (90y - 100) => 100 = 90y - 9 x.
90y - 9 x = 100 (person - 2 is walk fast).
90y - 10 x= 50 (equ 2 is multiplied by 10).
------------------
x = 50.
------------------
Equ 2 is => x = (9y - 10) /9 *10.
9 x = (9y - 10) * 10.
9x = (90y - 100) => 100 = 90y - 9 x.
90y - 9 x = 100 (person - 2 is walk fast).
90y - 10 x= 50 (equ 2 is multiplied by 10).
------------------
x = 50.
------------------
Raja said:
9 years ago
@K. Anitha.
I didn't get your last step. Please explain.
I didn't get your last step. Please explain.
Akhilesh Mehta said:
9 years ago
@Karuna.
It is for converting the speed Km/h to m/sec.
It is for converting the speed Km/h to m/sec.
Karuna said:
9 years ago
What is that 5/18 and why should we take that?
Soundarya said:
10 years ago
@Kabil.
How is 55/9 is coming?
How is 55/9 is coming?
Durga said:
10 years ago
Please anyone can simplify this step?
9y-x=5 and 90y-9x=100. I can't understand this. How will we get x=50?
9y-x=5 and 90y-9x=100. I can't understand this. How will we get x=50?
Alpesh jiwane said:
1 decade ago
What is the speed of a train if it overtakes two persons who are walking in the same direction at the rate of a m/s, (a+1) m/s, and passes them completely in b second and (b+1) seconds respectively?
Ravi said:
1 decade ago
Please any one can simply this step by step x/(y-10/9) = 10.
How can we get 10(9y-10) = 9x?
How can we get 10(9y-10) = 9x?
Javid Mir said:
1 decade ago
There are two cases:
In the first case, speed of man = 2 km/h => 2x5/18 => 5/9 m/sec.
Therefore, relative speed of train we know that first train (let speed of train be 'V') ,
V-5/9 = L/9....(1) here 'L' is length of train.
Now, for 2nd case, speed of man = 4 km/h => 4x5/18 => 10/9 m/sec.
Therefore, V-10/9 = L/10....(2).
From equation (1) we get,
9V-5/9 = L/9.
Cut denominator 9 on both side we get.
9V-5 = L or 9V = L+5 or V = (L+5) /9.
Now substituting the value of V in equation --- (2).
(L+5) /9 - 10/9 = L/10.
L+5-10/9 = L/10.
L+5-10 = 9L/10.
On cross multiplication,
10L+50-100 = 9L.
On rearranging.
10L-9L = 100-50.
L = 50 meters.
In the first case, speed of man = 2 km/h => 2x5/18 => 5/9 m/sec.
Therefore, relative speed of train we know that first train (let speed of train be 'V') ,
V-5/9 = L/9....(1) here 'L' is length of train.
Now, for 2nd case, speed of man = 4 km/h => 4x5/18 => 10/9 m/sec.
Therefore, V-10/9 = L/10....(2).
From equation (1) we get,
9V-5/9 = L/9.
Cut denominator 9 on both side we get.
9V-5 = L or 9V = L+5 or V = (L+5) /9.
Now substituting the value of V in equation --- (2).
(L+5) /9 - 10/9 = L/10.
L+5-10/9 = L/10.
L+5-10 = 9L/10.
On cross multiplication,
10L+50-100 = 9L.
On rearranging.
10L-9L = 100-50.
L = 50 meters.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers