Online Engineering Mechanics Test - Engineering Mechanics Test 10
- This is a FREE online test. Beware of scammers who ask for money to attend this test.
- Total number of questions: 20.
- Time allotted: 30 minutes.
- Each question carries 1 mark; there are no negative marks.
- DO NOT refresh the page.
- All the best!
Marks : 2/20
Test Review : View answers and explanation for this test.
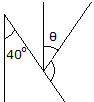
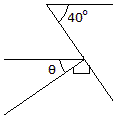
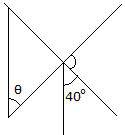
Determine the angle
: = 30° = 40° = 60° = 50°
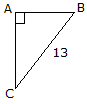
Determine the length of side AB if right angle ABC is similar to right angle A'B'C':
Using the basic trigonomic functions, determine the length of side AB of the right triangle.
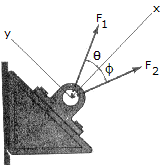
If = 20° and 
= 35°, determine the magnitudes of F1 and F2 so that the resultant force has a magnitude of 20 lb and is directed along the positive x axis.
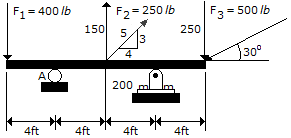
Determine the moment of force F2 about point A on the beam.
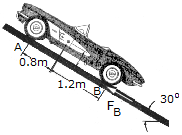
The sports car has a mass of 1.5 Mg and mass center at G. If the front two springs each have a stiffness of kA=58 kN/m and the rear two springs each have a stiffness of kB = 65 kN/m, determine their compression when the car is parked on the 30° incline. Also, what frictional force FB must be applied to each of the rear wheels to hold the car in equilibrium?
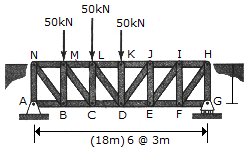
The Pratt bridge truss is subjected to the loading shown. Determine the force in members CD, CL and ML, and indicate whether these members are in tension or compression.
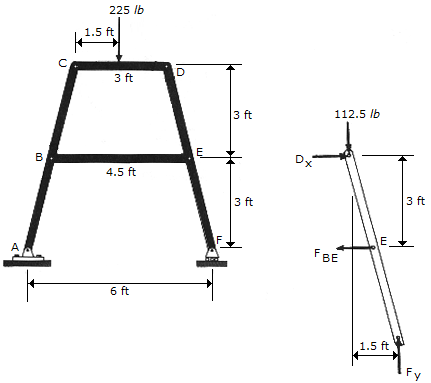
Determine the magnitude of the forces in pins B and D of the four-member frame.
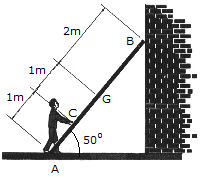
A 17-kg ladder has a center of mass at G. If the coefficients of friction at A and B are 
A = 0.3 and B = 0.2, respectively, determine the smallest horizontal force that the man must exert of the ladder at point C in order to push the ladder forward.
The refrigerator has a weight of 200 lb and a center of gravity at G. Determine the force P required to move it. Will the refrigerator tip or slip? Take = 0.4.
The boy at D has a mass of 50 kg, a center of mass at G, and stands on a plank at the position shown. The plank is pin-supported at A and rests on a post at B. Neglecting the weight of the plank and post, determine the magnitude of force P his friend (?) at E must exert in order to pull out the post. Take B = 0.3 and C = 0.8.
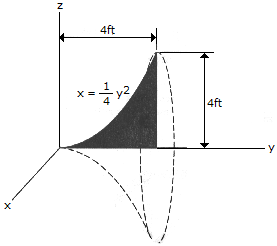
Locate the center of gravity of the homogeneous "bell-shaped" volume formed by revolving the shaded area about the y axis.
= 3.33 ft = 2.80 ft = 3.20 ft = 3.00 ft
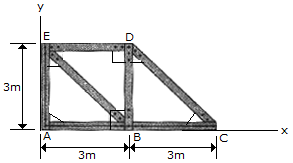
The truss is made from seven members, each having a mass of 6 kg/m. Locate the position (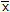
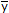,) of the center of mass. Neglect the mass of the gusset plates at the joints.
= 2.36 m, = 1.286 m = 2.33 m, = 1.333 m = 2.43 m, = 1.308 m = 2.79 m, = 1.757 m
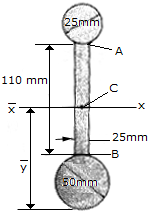
Determine the distance 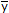to the centroid axis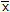 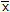of the beam's cross-sectional area. Neglect the size of the corner welds at A and B for the calculation.
= 75.2 mm = 97.5 mm = 85.9 mm = 102.5 mm
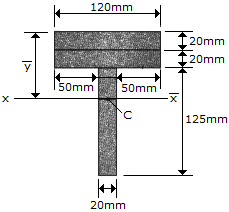
Determine the location 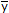of the centroid C of the beam's cross-sectional area. Then compute the moment of inertia of the area about the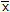 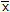axis.
= 48.3 mm, I = 15.08(106) mm4 = 48.3 mm, I = 15.08(106) mm4 = 48.3 mm, I = 15.08(106) mm4 = 48.3 mm, I = 15.08(106) mm4
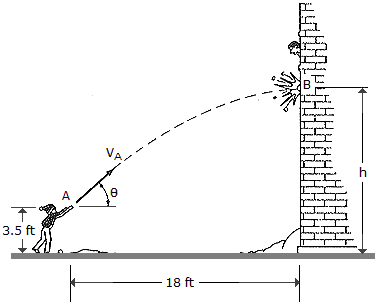
The boy throws a snowball such that it strikes the wall of the building at the maximum height of its trajectory. If it takes t = 1.5 s to travel from A to B, determine the velocity vA at which it was thrown, the angle of release , and the height h.
= 24.4E, h = 21.7 ft = 76.0E, h = 39.7 ft = 24.4E, h = 18.2 ft = 65.6E, h = 39.7 ft
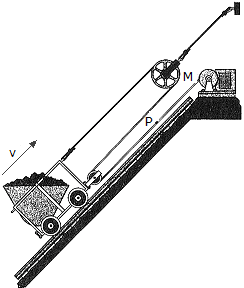
The mine car is being pulled up to the inclined plane using the motor M and the rope-and-pulley arragement shown. Determine the speed vp at which a point P on the cable must be traveling toward the motor to move the the car up the plane with a constant speed of v = 5 m/s.
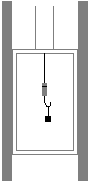
A block having a mass of 2 kg is placed on a a spring scale located in an elevator that is moving downward. If the scale reading, which measures the force in the spring, is 20 N, determine the acceleration of the elevator. Neglect the mass of the scale.
A ball having a mass of 2 kg slides without friction within a vertical circular slot. If it is released from rest when = 10°, determine the force it exerts on the slot when it arrives at points A and B.
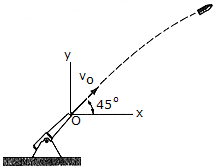
The projectile having a mass of m = 3 kg is fired from a cannon with a muzzle velocity of vO = 500 m/s. Determine the projectile's angular momentum about point O at the instant it is at the maximum height of its trajectory.