Engineering Mechanics - General Principles - Discussion
Discussion Forum : General Principles - General Questions (Q.No. 7)
7.
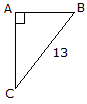

Determine the length of side AB if right angle ABC is similar to right angle A'B'C':
Discussion:
9 comments Page 1 of 1.
ADITYA KASHYAP said:
6 years ago
b'c'= square root 36^2+15^2=39 we get;
B'C'\BC=AC\A'C' THEN WE GET AC=13*36 \39=12.
c=12.
AB= √ 13^2-12^2=5 ANS.
B'C'\BC=AC\A'C' THEN WE GET AC=13*36 \39=12.
c=12.
AB= √ 13^2-12^2=5 ANS.
(1)
Nayan said:
1 decade ago
(B'C')^2 = (A'C')^2+(A'B')^2.
B'C' = sqrt[(36)^2+(15)^2].
B'C' = 39.
From Similar Triangles,
AB/A'B' = BC/B'C'.
AB = BC*A'B'/B'C'.
AB = 13*15/39.
AB = 5.
B'C' = sqrt[(36)^2+(15)^2].
B'C' = 39.
From Similar Triangles,
AB/A'B' = BC/B'C'.
AB = BC*A'B'/B'C'.
AB = 13*15/39.
AB = 5.
Shruti said:
1 decade ago
Is they are equilateral triangle?
Hamid alawi said:
1 decade ago
B'C' = 36^2 + 15^2 = 1521 square root = 39.
39/ 13 =3.
BC =13.
Now we get AC .
36/3 =12.
13 + 12 = 25 square root of 25 = 5.
39/ 13 =3.
BC =13.
Now we get AC .
36/3 =12.
13 + 12 = 25 square root of 25 = 5.
Ashwin said:
1 decade ago
B'C'=(36^2+15^2)^1/2
B'C'=39
From similar Triangles
BC/B'C' =13/39 =0.33333
AB=A'B' x 0.333 = 5.
B'C'=39
From similar Triangles
BC/B'C' =13/39 =0.33333
AB=A'B' x 0.333 = 5.
Kaushik gamit said:
1 decade ago
(36^2+15^2)^1/2=39
According to A'B'C'
tanx=36/15
x=67.38
is equals to <B
cos67.38=AB/BC=AB/13
So, AB=5
According to A'B'C'
tanx=36/15
x=67.38
is equals to <B
cos67.38=AB/BC=AB/13
So, AB=5
M.prakash said:
1 decade ago
How to solve this problem explain?
Saurabh khatri said:
1 decade ago
Here.
C'B'=39.
But CB=13.
So CB=1/3 part of C'B'.
Then AB=1/3 part of A'B' (triangles are similar).
So AB=5.
C'B'=39.
But CB=13.
So CB=1/3 part of C'B'.
Then AB=1/3 part of A'B' (triangles are similar).
So AB=5.
NAVEEN said:
2 decades ago
B'C'=(36^2+15^2)^1/2
B'C'=39
From similar Triangles
AB/A'B' =13/39
AB=5
B'C'=39
From similar Triangles
AB/A'B' =13/39
AB=5
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers