Engineering Mechanics - Center of Gravity and Centroid - Discussion
Discussion Forum : Center of Gravity and Centroid - General Questions (Q.No. 2)
2.
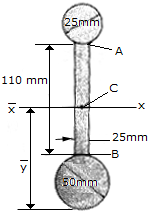
Determine the distance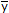 
to the centroid axis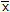 
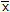of the beam's cross-sectional area. Neglect the size of the corner welds at A and B for the calculation.
= 75.2 mm = 97.5 mm = 85.9 mm = 102.5 mmDiscussion:
14 comments Page 1 of 2.
Girishkumar said:
2 years ago
According to me, the correct answer is 81.24mm.
(1)
Jdyoo said:
3 years ago
Does the centroid of individual sections match with the centroid of the built-up section?
Please explain.
Please explain.
Shashi said:
7 years ago
@Thompson Victor.
y3 is measured from base to half of the top circle. i.e dia 25 mm so half means 12.5mm
therefore from base 172.5= 50+110+12.5.
y3 is measured from base to half of the top circle. i.e dia 25 mm so half means 12.5mm
therefore from base 172.5= 50+110+12.5.
Thompson victor said:
7 years ago
Please tell, how did you get y3?
Ajit Kumar said:
8 years ago
81.20 is the correct answer.
Mithun Raju N said:
9 years ago
However the nearest available option is 85.9 for 81.18. So we need select the option C.
Prashant said:
9 years ago
I think 81.2 mm is the correct answer.
Abhishek Sharma said:
9 years ago
The Correct answer is 81.18647324...
Jaspreet singh nagpal said:
9 years ago
My Answer does not match with the given options.
The correct answer is 81.19 please do check the calculations once again.
The correct answer is 81.19 please do check the calculations once again.
Dharmalingam Ramasamy said:
9 years ago
a1 = pixr^2 = pix25^2 = 1963.5;
a2 = 110 * 25 = 2750;
a3 = pixr^2 = pix12.5^2 = 491;
y1 = 25; y2 = 105; y3 = 172.5.
= (a1y1 + a2y2 + a3y3) / (a1 + a2 + a3) = 85mm.
a2 = 110 * 25 = 2750;
a3 = pixr^2 = pix12.5^2 = 491;
y1 = 25; y2 = 105; y3 = 172.5.
= (a1y1 + a2y2 + a3y3) / (a1 + a2 + a3) = 85mm.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers