Online Engineering Mechanics Test - Engineering Mechanics Test 6
- This is a FREE online test. Beware of scammers who ask for money to attend this test.
- Total number of questions: 20.
- Time allotted: 30 minutes.
- Each question carries 1 mark; there are no negative marks.
- DO NOT refresh the page.
- All the best!
Marks : 2/20
Test Review : View answers and explanation for this test.
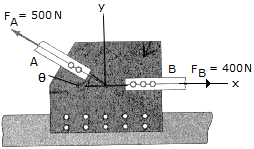
Determine the design angle 
for connecting member A to the plate if the resultant force is to be directed vercially upward. Also, what is the magnitude of the resultant?
= 53.5° = 30.0° = 36.9° = 38.6°
Two forces act on a block. Determine the angle between them.
= 135.0° = 65.1° = 45.0° = 114.9°
A "scale" is constructed with a 4-ft-long cord and the 10-lb block D. The cord is fixed to a pin at A and passes over two small pulleys at B and C. Determine the weight of the suspended block E if the system is in equilibrium when s = 1.5 ft.
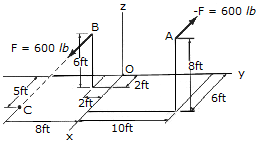
Determine the couple moment. Use a vector analysis and express the result as a Cartesian vector.
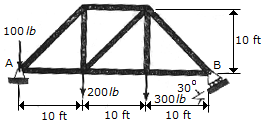
Determine the horizontal and vertical components of reaction at the pin A and the reaction at the roller support B required for equilibrium of the truss.
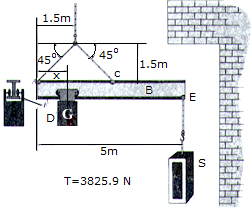
If the boom in the previous problem is to remain horizontal when the stone S is removed, what is x?
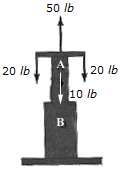
The axial forces act on the shaft as shown. Determine the internal axial force at points A and B.
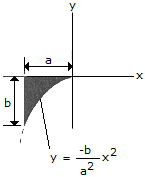
Locate the centroid of the exparabolic segment of area.
= -4a/5, 
= -b/4 = -3a/4, = -3b/10 = -2a/3, = -b/3 = -5a/7, = -3b/8
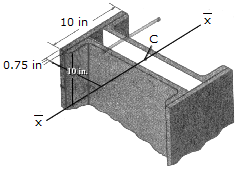
The composite cross section for the column consists of two cover plates riveted to two channels. Determine the radius of gyration k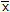 with respect to the centroidal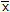 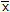axis. Each channel has a cross-sectional area of Ac = 11.8 in.2 and moment of inertia (I 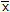)c = 349 in.4.
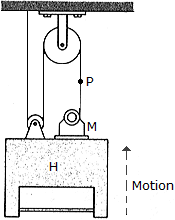
If the hoist H is moving upward at 6 ft/s, determine the speed at which the motor M must draw in the supporting cable.
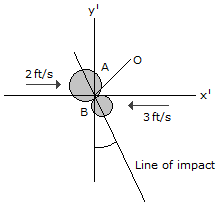
Two coins A and B have the initial velocities shown just before they collide at point O. If they have weights of WA = 13.2(10-3) lb and WB = 6.6(10-3) lb and the surface upon which they slide is smooth, determine their speed just after impact. The coefficient of restitution is e = 0.65.
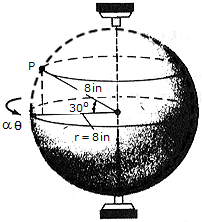
The sphere starts from rest at = 0 and rotates with an angular acceleration of 
= (4) rad/s2, where is measured in radians. Determine the magnitudes of the velocity and acceleration of point P on the sphere at the instant = 6 rad.
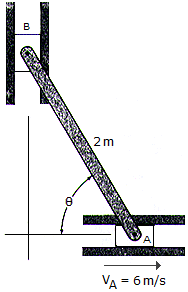
The 2-m-long bar is confined to move in the horizontal and vertical slots A and B. If the velocity of the slider block at A is 6 m/s, determine the bar's angular velocity and the velocity of block B at the instant = 60°.
AB = 3.46 rad/s 
, vB = 3.46 m/s 9AB = 3.00 rad/s , vB = 3.00 m/s 9AB = 3.00 rad/s , vB = 6.00 m/s 9AB = 6.00 rad/s , vB = 10.39 m/s 9
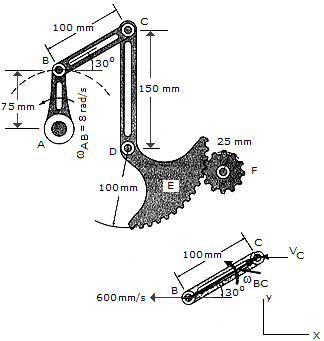
The rotation of link AB creates an oscillating movement of gear F. If AB has an angular velocity of AB = 8 rad/s, determine the angular velocity of gear F at the instant shown. Gear E is a part of arm CD and pinned at D to a fixed point.
F = 26.7 rad/sF = 16.00 rad/sF = 32.0 rad/sF = 27.7 rad/s
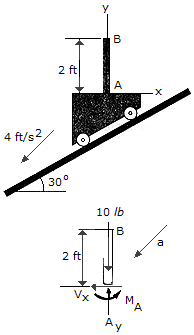
Bar AB has a weight of 10 lb and is fixed to the carriage at A. Determine the internal axial force Ay, shear force V
, and moment MA at A if the carriage is descending the plane with an acceleration of 4 ft/s2.
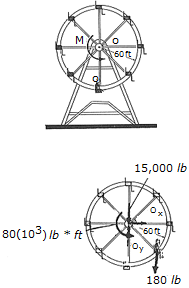
A man having a weight of 180 lb sits in a chair of the Ferris wheel, which has a weight of 15,000 lb and a radius of gyration of ko = 37 ft. If a torque of M = 80(103) lb • ft is applied about O, determine the angular velocity of the wheel after it has rotated 180°. Neglect the weight of the chairs and note that the man remains in an upright position as the wheel rotates. The wheel starts from rest in the position shown.
= 0.888 rad/s = 0.836 rad/s = 0.874 rad/s = 0.849 rad/s
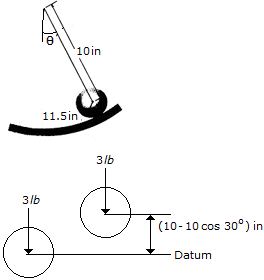
If the 3-lb solid sphere is released from rest when = 30°, determine its angular velocity when = 0°, which is the lowest point of the curved path having a radius of 11.5 in. The sphere does not slip as it rolls.
= 15.17 rad/s = 18.13 rad/s = 21.5 rad/s = 17.15 rad/s
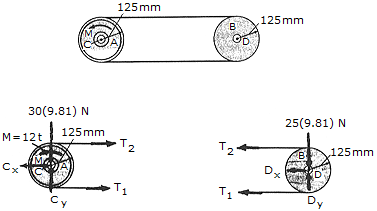
The flywheel A has a mass of 30 kg and a radius of gyration of kc = 95 mm. Disk B has a mass of 25 kg, is pinned at D, and is coupled to the flywheel using a belt which is subjected to a tension such that it does not slip at its contacting surfaces. If a motor supplies a counter-clockwise torque or twist to the flywheel, having a magnitude of M = (12t) N • m, where t is measured in seconds, determine the angular velocity of the disk 3 s after the motor is turned on. Initially, the flywheel is at rest.
= 232 rad/s = 77.2 rad/s = 115.9 rad/s = 276 rad/s
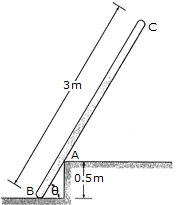
The uniform pole has a mass of 15 kg and falls from rest when = 90° until it strikes the edge at A, = 60°. If the pole then begins to pivot about this point after contact, determine the pole's angular velocity just after the impact. Assume that the pole does not slip at B as it falls until it strikes A.
3 = 1.146 rad/s3 = 0.537 rad/s3 = 2.15 rad/s3 = 1.528 rad/s