Engineering Mechanics - Planar Kinematics of a Rigid Body (PKRB) - Discussion
Discussion Forum : Planar Kinematics of a Rigid Body (PKRB) - General Questions (Q.No. 2)
2.
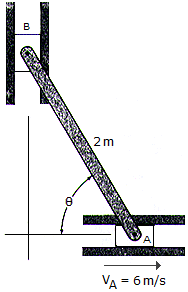
The 2-m-long bar is confined to move in the horizontal and vertical slots A and B. If the velocity of the slider block at A is 6 m/s, determine the bar's angular velocity and the velocity of block B at the instant 
= 60°.
AB = 3.46 rad/s 
, vB = 3.46 m/s 9AB = 3.00 rad/s , vB = 3.00 m/s 9AB = 3.00 rad/s , vB = 6.00 m/s 9AB = 6.00 rad/s , vB = 10.39 m/s 9Discussion:
4 comments Page 1 of 1.
Pankaj said:
4 years ago
Vb - Va=Vba.
Vba = wrba.
Vb - va = w rba.
Vb = 6i + w*2(-cos60i +sin60j).
Vb is in y direction so we only take y component and it's x component should be zero
Vb = 2wsin60, 6-2wcos60=0.
w = 6/(2cos60).
w = 6,
Vb = 2 * 6 * √3/2.
Vb = 6√3,
Vb = 10.39.
Vba = wrba.
Vb - va = w rba.
Vb = 6i + w*2(-cos60i +sin60j).
Vb is in y direction so we only take y component and it's x component should be zero
Vb = 2wsin60, 6-2wcos60=0.
w = 6/(2cos60).
w = 6,
Vb = 2 * 6 * √3/2.
Vb = 6√3,
Vb = 10.39.
Jani Dhruvkumar said:
6 years ago
No, the Correct one is;
Hence both points are on single link AB, therefore, the value of w=wa=wb.
Now,
W=(Va/Ia)=(Vb/Ib).
(Va=6m/s).
(Ia=√3 and Ib=1 from instantaneous centre method).
Therefore wb=wa=w=3.46.
Hence both points are on single link AB, therefore, the value of w=wa=wb.
Now,
W=(Va/Ia)=(Vb/Ib).
(Va=6m/s).
(Ia=√3 and Ib=1 from instantaneous centre method).
Therefore wb=wa=w=3.46.
Rios said:
8 years ago
Doing a triangle, the displacement is equal to 2 sin(60).
VA= wr.
6= w(2sin(60)).
w=3.46.
VA= wr.
6= w(2sin(60)).
w=3.46.
Arpit lasod said:
1 decade ago
consider rod AB, and A as I.C.R.(instantenous center of rotation)
Va=6m/s
r=2m(length of the rod)
Va=rw
w=3rad/s
consider rod AB, and B as I.C.R.(instantenous center of rotation)
r=2m
w=3rad/s
Vb=rw
Vb=6m/s
Va=6m/s
r=2m(length of the rod)
Va=rw
w=3rad/s
consider rod AB, and B as I.C.R.(instantenous center of rotation)
r=2m
w=3rad/s
Vb=rw
Vb=6m/s
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers