Engineering Mechanics - Structural Analysis - Discussion
Discussion Forum : Structural Analysis - General Questions (Q.No. 1)
1.
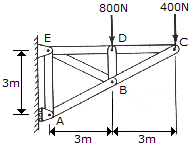
Determine the force in each member of the truss and indicate whether the members are in tension or compression.
Discussion:
7 comments Page 1 of 1.
Bakri said:
8 years ago
How do you end up with sum of horizontal forces as Re(x)-800-400? Please explain @Prince Tetteh.
(1)
Hasmukh vasava said:
8 years ago
I don't understand how to arrive sin and cos (26.57) in summation of vertical forcer and sin and cos (63.43) in horizontal forces. Please help me to get it.
Mamdooh said:
10 years ago
Thank you, @Prince Tetteh.
I will solve it in my assignment.
I will solve it in my assignment.
Prince tetteh said:
1 decade ago
Ok guys.
First consider a free body diagram for the whole truss structure to find the reactions at supports E and A by applying the equations of equilibrium for its external forces.
So taking summation of moment about E = 0, 3Ra-3(800)-6(400) = 0.
Ra = 1600 N.
Sum of horizontal forces = Re(x)-800-400 = 0; Re(x) = 1200 N.
Sum of vertical forces = Re(y)-Ra = 0; Re(y) = 1600 N.
Considering each member force to be a tension, each joint will be analyzed so taking joint C,
Sum of horizontal forces = 400+F(CB) sin(26.57) = 0, F(CB) = -894 N T or F(CB) = 894 N C.
Sum of vertical forces = -F(CB) cos (26.57)-F(CD) = 0; F(CD) = 800 N T.
At joint D, F(DC) = F(DE) = 800 N T F(DB) = -800 N T = 800 N C.
At joint E, Sum of vertical forces = F ED)+F(EB) sin(63.43)-Re(y) = 0.
F(EB) = (Re(Y)-F(ED))/sin(63.43) = 894 N T.
Sum of horizontal forces = F(EA) = F(EB) cos(63.43) = Re(x).
F(EA) = 1200-894 cos(63.43) = 800 N T.
At joint B, Sum of horizontal forces = 0.
F(BA) cos(63.43)-F(BC) cos(63.43)-F(BE) cos(63.43)-F(BD) = 0.
F (BA) = -1789 N T = 1789 N C.
First consider a free body diagram for the whole truss structure to find the reactions at supports E and A by applying the equations of equilibrium for its external forces.
So taking summation of moment about E = 0, 3Ra-3(800)-6(400) = 0.
Ra = 1600 N.
Sum of horizontal forces = Re(x)-800-400 = 0; Re(x) = 1200 N.
Sum of vertical forces = Re(y)-Ra = 0; Re(y) = 1600 N.
Considering each member force to be a tension, each joint will be analyzed so taking joint C,
Sum of horizontal forces = 400+F(CB) sin(26.57) = 0, F(CB) = -894 N T or F(CB) = 894 N C.
Sum of vertical forces = -F(CB) cos (26.57)-F(CD) = 0; F(CD) = 800 N T.
At joint D, F(DC) = F(DE) = 800 N T F(DB) = -800 N T = 800 N C.
At joint E, Sum of vertical forces = F ED)+F(EB) sin(63.43)-Re(y) = 0.
F(EB) = (Re(Y)-F(ED))/sin(63.43) = 894 N T.
Sum of horizontal forces = F(EA) = F(EB) cos(63.43) = Re(x).
F(EA) = 1200-894 cos(63.43) = 800 N T.
At joint B, Sum of horizontal forces = 0.
F(BA) cos(63.43)-F(BC) cos(63.43)-F(BE) cos(63.43)-F(BD) = 0.
F (BA) = -1789 N T = 1789 N C.
(1)
Fahim said:
1 decade ago
By using method of joints, i can get CB CD DB and DE, but when doing joint B i get the wrong answer. Can anyone help? Thanks in advance.
(i know i have enough to answer the question, but i would like to be able to work through the whole thing)
(i know i have enough to answer the question, but i would like to be able to work through the whole thing)
Md waseem said:
1 decade ago
Please exlain us.
Aravinth said:
1 decade ago
Please give explaination also.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers