Engineering Mechanics - Kinematics of Particle (KOP)
- Kinematics of Particle (KOP) - General Questions
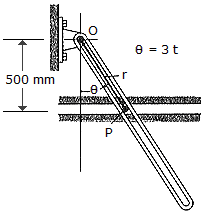
The slotted link is pinned at O, and as a result of rotation it drives the peg P along the horizontal guide. Compute the magnitude of the velocity and acceleration of P along the horizontal guide. Compute the magnitudes of the velocity and acceleration of P as a function of 
if = (3t) rad, where t is measured in seconds.
m/s, a = 1.000 sec2 tan m/s2 m/s, a = 9.00 sec tan m/s2 tan m/s, a = 9.00 sec tan m/s2 m/s, a = 9.00 sec2 tan m/s2
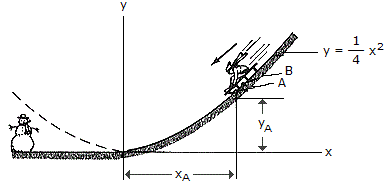
A sled is traveling down along a curve which can be approximated by the parabola y =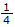 
x2. When point B on the runner is coincident with point A on the curve (xA = 2m, yA = 1 m), the speed if B is measured as vB = 8 m/s and the increase in speed is dvB/dt = 4 m/s2. Determine the magnitude of the acceleration of point B at this instant.
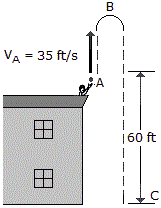
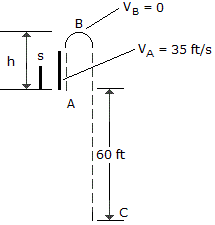
A ball thrown vertically upward from the top of a building with an initial velocity of vA = 35 ft/s. Determine (a) how high above the top of the building the ball will go before it stops at B, (b) the time tAB it takes to reach its maximum height, and (c) the total time tAC needed for it to reach the ground at C from the instant it is released.
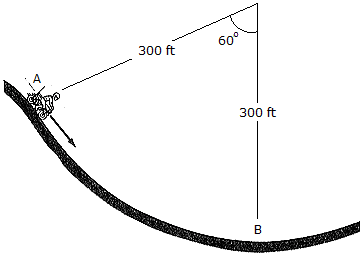
When the motorcyclist is at A he increases his speed along the vertical circular parth at the rate of v = (0.3t)ft/s2, where t is in seconds. If he starts from rest when he is at A, determine his velocity and acceleration when he reaches B.
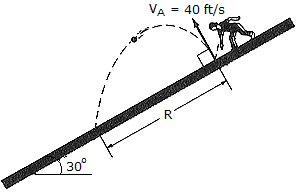
A ball is thrown downward on the 30° inclined plane so that when it rebounds perpendicular to the incline it has a velocity of vA = 40 ft/s. Determine the distance R where it strikes the plane at B.