Engineering Mechanics - Force Vectors - Discussion
Discussion Forum : Force Vectors - General Questions (Q.No. 3)
3.
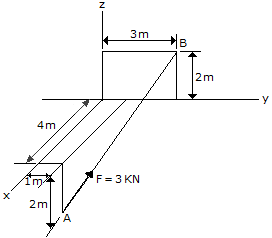
Express force F as a Cartesian vector; then determine its direction angles.
Discussion:
7 comments Page 1 of 1.
Hazim Khaleel said:
7 years ago
The right answer is D.
D Sanjog Roshan said:
8 years ago
A(4,1,-2) and B(0,3,2).
Position vector, Rab=-4i+2j+4k
Unit vector of Rab=-4/6i+2/6j+4/6k
F=3(Rab)= option B.
α=cos-1(-2/3)=131.8.
β=cos-1(1/3)=70.5.
γ=cos-1(2/3)=48.1.
Position vector, Rab=-4i+2j+4k
Unit vector of Rab=-4/6i+2/6j+4/6k
F=3(Rab)= option B.
α=cos-1(-2/3)=131.8.
β=cos-1(1/3)=70.5.
γ=cos-1(2/3)=48.1.
.shinde mahesh said:
1 decade ago
I thing its very lengthy process. Any one can give shortcuts for this problem?
Wahid said:
1 decade ago
A(4;1;-2) & B(0;3;2) then vect(AB) = 2(-2i+j+2k)and,
180-cos(a) = 2/AB then a = 131.8.
cos(b) = 1/AB then b = 70.5.
cos(c) = 2/AB then c = 48.2.
180-cos(a) = 2/AB then a = 131.8.
cos(b) = 1/AB then b = 70.5.
cos(c) = 2/AB then c = 48.2.
Avinash said:
1 decade ago
Write the position vectors B and A. Then do A-B. Result is the vector direction.
Benjamin said:
1 decade ago
I am relearning a lot of maths and if there is anyone about that can write an method I would be very greatful, forgotten how this format works entirely.
Ramesh said:
1 decade ago
I want the explaination. I can't understand.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers
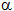 = 48.2°,
= 48.2°, 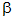 = 70.5°,
= 70.5°, 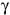 = 48.2°
= 48.2°