Engineering Mechanics - Force Vectors - Discussion
Discussion Forum : Force Vectors - General Questions (Q.No. 16)
16.
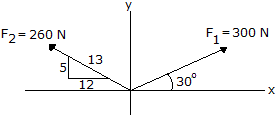
Determine the magnitude and direction of the resultant force.
Discussion:
4 comments Page 1 of 1.
Yoseph said:
1 decade ago
Clear but if it will be in parallelogram.
Rye said:
1 decade ago
Solving for the component of x
We have,
fx = [300cos30]+[-260x12/13]
fx = 20 N
Solving for fy:
fy=[300sin30]+[260x5/13]
fy=250 N
Therefore R=20squared+250square then taking its squareroot
R=251 N.
Solving for angle:
Angle =arctan fy/fx
Therefore:
Angle=arctan250/20.
Angle=85.5.
We have,
fx = [300cos30]+[-260x12/13]
fx = 20 N
Solving for fy:
fy=[300sin30]+[260x5/13]
fy=250 N
Therefore R=20squared+250square then taking its squareroot
R=251 N.
Solving for angle:
Angle =arctan fy/fx
Therefore:
Angle=arctan250/20.
Angle=85.5.
Khuliso said:
1 decade ago
The calculation are good, but is the any way we can do this?
Monica Ann said:
1 decade ago
First, solve for the angle of F2.
Let's have the angle as angle α (alpha).
That could be solved by using the sine law.
13/sin90= 5/sinα
Equating this gives us, α=22.61986495 degrees
Now, we can solve for F1x, F1y, F2x, F2y, Rx, Ry, R (resultant) and θ.
F1x= 300cos30
F1x= 259.8076211 N to the right
F1y= 300sin30
F1y= 150 N, up
F2x= -260cos22.61986495
F2x= 240 N to the left
F2y= 260sin22,61986495
F2y= 100 N, up
Rx= F1x+F2x
= [259.8076211 + (-240)]N
*Note that we have -F2x since the force is to the left.
Rx= 19.80762114 N
Ry= F1y + F2y
= [150 + 100]N
Ry= 250 N
R=*squareroot of [Rx*squared + Ry*squared]
=*squareroot of [(19.80...)*squared + (250)*squared]
=*squareroot of (392.3418552 + 62500)
=*squareroot of (62892.34186)
R=250.7834561 N, which could be rounded to 251 N.
θ= arctan (Ry/Rx)
= arctan (250/19.80...)
= arctan (12.62140457)
θ= 85.46989102 degrees, which could be rounded to 85.5 degrees.
Answer: 251 N, θ=85.5 degrees.
Let's have the angle as angle α (alpha).
That could be solved by using the sine law.
13/sin90= 5/sinα
Equating this gives us, α=22.61986495 degrees
Now, we can solve for F1x, F1y, F2x, F2y, Rx, Ry, R (resultant) and θ.
F1x= 300cos30
F1x= 259.8076211 N to the right
F1y= 300sin30
F1y= 150 N, up
F2x= -260cos22.61986495
F2x= 240 N to the left
F2y= 260sin22,61986495
F2y= 100 N, up
Rx= F1x+F2x
= [259.8076211 + (-240)]N
*Note that we have -F2x since the force is to the left.
Rx= 19.80762114 N
Ry= F1y + F2y
= [150 + 100]N
Ry= 250 N
R=*squareroot of [Rx*squared + Ry*squared]
=*squareroot of [(19.80...)*squared + (250)*squared]
=*squareroot of (392.3418552 + 62500)
=*squareroot of (62892.34186)
R=250.7834561 N, which could be rounded to 251 N.
θ= arctan (Ry/Rx)
= arctan (250/19.80...)
= arctan (12.62140457)
θ= 85.46989102 degrees, which could be rounded to 85.5 degrees.
Answer: 251 N, θ=85.5 degrees.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers
 = 85.5° CCW
= 85.5° CCW