Engineering Mechanics - Equilibrium of a Particle - Discussion
Discussion Forum : Equilibrium of a Particle - General Questions (Q.No. 1)
1.
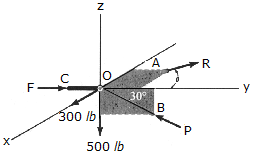
The joint O of a space frame is subjected to four forces. Strut OA lies in the x-y plane and strut OB lies in the y-z plane. Determine the force acting in each if the three struts required for equilibrium of the joint. Set  = 45°.
= 45°.
Discussion:
18 comments Page 1 of 2.
Narendra said:
5 years ago
How to solve it? Please explain.
(1)
Patience said:
8 years ago
Thank you for the explanation.
Raja said:
8 years ago
Thanks @Aditya.
HARI said:
8 years ago
Thanks @Aditya.
Chitti said:
9 years ago
Good job @Aditya.
Santosh kumar sahu said:
10 years ago
Good @Aditya, nice.
K.VISHNU said:
1 decade ago
300=R*sin45
R=424
500=P*sin30
P=1000
And
F=P*cos30-R*cos45
F=1000*Sqrt3/2-424/sqrt2
F=566
R=424
500=P*sin30
P=1000
And
F=P*cos30-R*cos45
F=1000*Sqrt3/2-424/sqrt2
F=566
Bikash said:
1 decade ago
Sum of forces in a direction =0
taking
E Fx=0;
E Fy=0;
E Fz=0;
Solve it simple.
taking
E Fx=0;
E Fy=0;
E Fz=0;
Solve it simple.
Sanatan Singh said:
1 decade ago
Why to convert the unit from lb to newton (N) when the answer required is in lb ?
Simple question just based on laws of static equilibrium.
Ex=0
Ey=0
Ez=0
Simple question just based on laws of static equilibrium.
Ex=0
Ey=0
Ez=0
Afiq said:
1 decade ago
How to convert lb to newton?
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers