Electronics and Communication Engineering - Signals and Systems - Discussion
Discussion Forum : Signals and Systems - Section 1 (Q.No. 4)
4.
Consider Pole zero diagram as shown, If two Poles are moved in opposite direction towards ω = p/2 and -p/2, the filter will be


Answer: Option
Explanation:
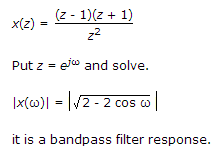


But still we will get the same response, zero are at same position.
Discussion:
13 comments Page 1 of 2.
Neal said:
5 years ago
Not getting a clear solution. Anyone explain.
Fatima noor said:
6 years ago
Zeros are same but poles are changed. Then How we get the same response?
Geetha said:
7 years ago
I didn't understand, Please anyone, explain me.
Lavanya said:
7 years ago
I am not getting this, can anyone explain me in clear?
Rachana said:
7 years ago
Thank you all for providing best explanation.
K.ramesh said:
8 years ago
What is the LPF?
Kishore said:
8 years ago
In denominator how did z^2 came, poles should come in denominator and zeroes should come in the numerator. Explain me clearly.
Ghanshyam said:
9 years ago
How does it take to pole at the origin?
Bibo said:
10 years ago
For digital domain, in low frequency w = 0 hence z = exp(j0) = 1.
High-frequency w = pi, z = -1 now put z = 1 and -1 and find response, you will get zero every time.
Hence, both are Band Pass filter.
High-frequency w = pi, z = -1 now put z = 1 and -1 and find response, you will get zero every time.
Hence, both are Band Pass filter.
Neha said:
1 decade ago
If you consider x(z) = (z-1)(z+1)/z2.
Then if z = ejw = cosw + jsinw.
Then x(ejw) = (e2jw - 1)/e2jw.
Now magnitude is X(w) = ((Cos 2w-1)2 + (sin 2w)2) 1/2.
As magnitude = (Real 2+image 2) 1/2.
So the plot is given for its magnitude similarly when you change the poles there won't be change in magnitude, hence filter remains the same.
Hope you will understand this.
Then if z = ejw = cosw + jsinw.
Then x(ejw) = (e2jw - 1)/e2jw.
Now magnitude is X(w) = ((Cos 2w-1)2 + (sin 2w)2) 1/2.
As magnitude = (Real 2+image 2) 1/2.
So the plot is given for its magnitude similarly when you change the poles there won't be change in magnitude, hence filter remains the same.
Hope you will understand this.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers