Electronics and Communication Engineering - Networks Analysis and Synthesis - Discussion
Discussion Forum : Networks Analysis and Synthesis - Section 1 (Q.No. 31)
31.
In the series circuit shown in figure, for series resonance, the value of the coupling coefficient, K will be
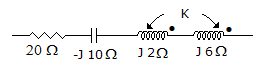

Answer: Option
Explanation:
Mutual inductance wm = ωk L1L2
 m = k. 2. 8j2 = 4k. j
m = k. 2. 8j2 = 4k. j
Z = 20 - j10 + j2 + j6 + 2.4kj - 2j + 8kj = 0 at resonance
 -2 = -8k
-2 = -8k
k = 1/4  0.25 .
0.25 .
Discussion:
8 comments Page 1 of 1.
Ahmad said:
1 decade ago
Can you tell me where did the 2.4kj-2j+8kj came from?
(1)
Krishnasai said:
1 decade ago
Network Theory works in mysterious ways.
(1)
Vini said:
1 decade ago
Do it by xl=xc no need of r!
(1)
Gopi said:
10 years ago
@Vini still I didn't get you. Please tell me the whole answer.
(1)
Prateek rajput said:
9 years ago
In the case of resonance XL = XC not z = 0.
(1)
Dheeraj said:
9 years ago
According to me, nswer should be 0.2886.
(1)
RusselRV said:
6 years ago
M = k* sqrt[ (j 2)(j 6)] = k*j*3.464.
at resonance |Xc| = |XL|.
|XL| = XL1 + XL2 + 2 Xm.
= j 2 + j 6 + 2( k* j* 3.464).
|Xc| = -j 10,
j10 = j 8 + 2k* j* 3.464.
k= 0.2886.
at resonance |Xc| = |XL|.
|XL| = XL1 + XL2 + 2 Xm.
= j 2 + j 6 + 2( k* j* 3.464).
|Xc| = -j 10,
j10 = j 8 + 2k* j* 3.464.
k= 0.2886.
RISHI NIGAM said:
4 years ago
At resonance, resistance will only exist so total inductive and capacitive reactance should be equal now there is dot convention so first try to find the equivalent inductance for that find that dot is supporting or opposing because ever have different like supporting have l1+l2+2m and opposing l1+l2-2m and this is for inductance in series and if they are in parallel then l1l2-m^2/l1+l2+2m and similarly for parallel supporting.
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers